これまで述べたのは単成分系(純物質)におけるフュガシティの定式化についてであった。この章の最終目的は多成分系(混合物)の相平衡を求めることだったので、多成分系のフュガシティに拡張する必要がある。
結論から述べると、多成分系における成分![]() のフュガシティは次のように定式化することができる。
のフュガシティは次のように定式化することができる。
(25) ![]()
または、
(26) ![]()
ただし、![]() は系全体の体積を、記号「
は系全体の体積を、記号「![]() 」は成分
」は成分![]() の部分モル体積を表している。部分モル体積は、部分モル量という概念の一種である。部分モル量とは、状態量を成分
の部分モル体積を表している。部分モル体積は、部分モル量という概念の一種である。部分モル量とは、状態量を成分![]() の物質量で偏微分したものであり、例えば部分モル体積partial molar volumeは次のように与えられる。
の物質量で偏微分したものであり、例えば部分モル体積partial molar volumeは次のように与えられる。
(27) ![]()
それでは、式展開を追って実際に多成分系のフュガシティを導出してみよう。まず![]() 成分系を仮定すると、ギブズエネルギーの全微分は次のように書けることはすでに示した。
成分系を仮定すると、ギブズエネルギーの全微分は次のように書けることはすでに示した。
(28) ![]()
数学的な要請として、上式が![]() の全微分であるための必要条件は、
の全微分であるための必要条件は、
(29) ![]()
であるが、(28)式はあらかじめ![]() の全微分であることが示されているので、(29)式は常に成り立つ。したがって今後この式を出発点にすることとする。なぜこのような式が導けるかについては別途まとめたので参照してほしい。さて、(27)式と(29)式を組み合わせると、次の式を得ることができる。
の全微分であることが示されているので、(29)式は常に成り立つ。したがって今後この式を出発点にすることとする。なぜこのような式が導けるかについては別途まとめたので参照してほしい。さて、(27)式と(29)式を組み合わせると、次の式を得ることができる。
(30) ![]()
化学ポテンシャル![]() は温度
は温度![]() と圧力
と圧力![]() の関数であったわけだが、
の関数であったわけだが、![]() が一定であれば
が一定であれば![]() のみの関数となって、偏微分記号を使う必要がなくなる。すると次のような形が導ける。
のみの関数となって、偏微分記号を使う必要がなくなる。すると次のような形が導ける。
(31) ![]()
ここで、成分![]() の化学ポテンシャルを表現すると、前章(136)式より
の化学ポテンシャルを表現すると、前章(136)式より
(32) ![]()
と与えられていることを思い出して、この式の両辺から![]() を引いて変形すると次の式が得られる。
を引いて変形すると次の式が得られる。
(33) 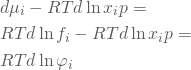
ただし、![]() は成分
は成分![]() のモル分率(成分
のモル分率(成分![]() の分子数/系全体の総分子数)、
の分子数/系全体の総分子数)、![]() は成分
は成分![]() のフュガシティ係数、
のフュガシティ係数、![]() は系の全圧であり、変形には前章(140)式で示されている以下関係を使った。
は系の全圧であり、変形には前章(140)式で示されている以下関係を使った。
(34) ![]()
さて、(33)式をさらに変形するにあたって、左辺第二項に注目すると、
(35) ![]()
の形が導けることがすぐに分かるが、![]() は閉じた系において成分
は閉じた系において成分![]() の分子数と、系に含まれる全分子数がそれぞれ一定であることから、常に0になるため、結局次の関係が得られる。
の分子数と、系に含まれる全分子数がそれぞれ一定であることから、常に0になるため、結局次の関係が得られる。
(36) ![]()
この式を(33)式に代入すると次の式が得られる。
(37) ![]()
また、左辺第一項は(31)式を用いると部分モル体積を使って表現できるので結局、
(38) ![]()
なる式を得ることができる。ここまで来ると、あとは両辺を適当な区間で積分すればよい。
(39) ![]()
この積分についての詳細な式展開は、単成分系におけるフュガシティの定式化ですでに紹介してあり、冗長になるのでここでは省いた。上式を![]() で割って形を整えると、多成分系におけるフュガシティの導出式として提示した二式のうち体積に明示的volume explicitな表示のものを導くことができる。
で割って形を整えると、多成分系におけるフュガシティの導出式として提示した二式のうち体積に明示的volume explicitな表示のものを導くことができる。
(40) ![]()
続いて、単成分系での議論と同じように、圧力に明示的pressure explicitな形式を導くことにする。![]() の代わりに
の代わりに![]() に明示的な式で表そう魂胆なので、
に明示的な式で表そう魂胆なので、![]() と
と![]() を結び付けている状態方程式を出発点にする。まずは復習であるが、zファクターについての状態方程式を表現すると、
を結び付けている状態方程式を出発点にする。まずは復習であるが、zファクターについての状態方程式を表現すると、
(41) ![]()
である。温度![]() と物質量
と物質量![]() が一定であると仮定してこの式の全微分をとると次のような式が得られる。
が一定であると仮定してこの式の全微分をとると次のような式が得られる。
(42) ![]()
この両辺に![]() を掛ける。
を掛ける。
(43) ![]()
ただし、
(44) ![]()
であるので、この関係を用いると次のような式を導くことができる。
(45) ![]()
また、自然対数の微分の公式によって次の関係が普遍的に成り立っている。
(46) ![]()
したがって、
(47) ![]()
であるので、この式を(45)式に代入して整理すると次が得られる。
(48) ![]()
次に、すでに成り立つことが分かっている(37)式、
(49) ![]()
に導いたばかりの(48)式を代入して形を整える。
(50) ![]()
さらにこの式の両辺を![]() で割って徐々に積分計算に持ち込む準備をする。
で割って徐々に積分計算に持ち込む準備をする。
(51) ![]()
順調に式変形が進んできたが、このままだと右辺第一項がこの先どうしても計算できないので、どうにかしようと思う。単成分系のときもそうだったが、全微分の必要十分条件を利用することで巧みに変数を変換していく。熱力学の章の表4よりヘルムホルツエネルギーの微分は
(52) ![]()
と与えられている。全微分についての数学的な議論より、上式がヘルムホルツエネルギーFの全微分であることの必要条件は、
(53) ![]()
であるが、(52)式はあらかじめ![]() の全微分であることが示されているので、(53)式は常に成り立つ。
の全微分であることが示されているので、(53)式は常に成り立つ。
行き詰っていた(51)式に上式を代入すると、次の式が得られる。
(54) ![]()
微分形式に変形するために![]() を両辺に掛けてさらに式を整えると次のように表現される。
を両辺に掛けてさらに式を整えると次のように表現される。
(55) 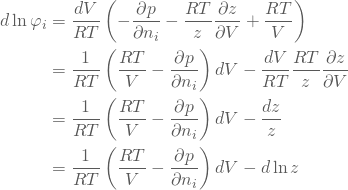
ただし、毎度の如く、
(56) ![]()
という自然対数の微分の公式を式変形に用いていることを注記しておく。
ここまで来ればあとは圧力について![]() から
から![]() までの区間で定積分をすればよく、次のように展開できる。
までの区間で定積分をすればよく、次のように展開できる。
(57) ![]()
なお、![]() のとき
のとき![]() 、
、![]() のとき
のとき![]() であるので、結局上式は次のような形に落ち着く。
であるので、結局上式は次のような形に落ち着く。
(58) ![]()
この式こそが多成分系でフュガシティを導出する大切な式である。また、ファン・デル・ワールス型の状態方程式の一般形をこの式に代入して整理すると以下の式を得ることができる。
![]()
(59) ![]()
![]()
この式は一般形であるので、具体的な例を挙げるとペン・ロビンソン状態方程式のフュガシティは次のように与えられる。
![]()
(60) ![]()
![]()








