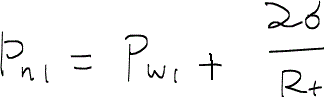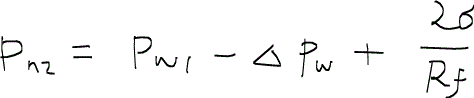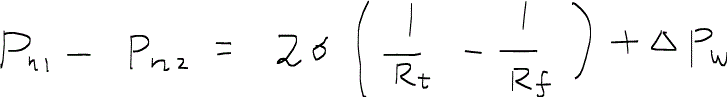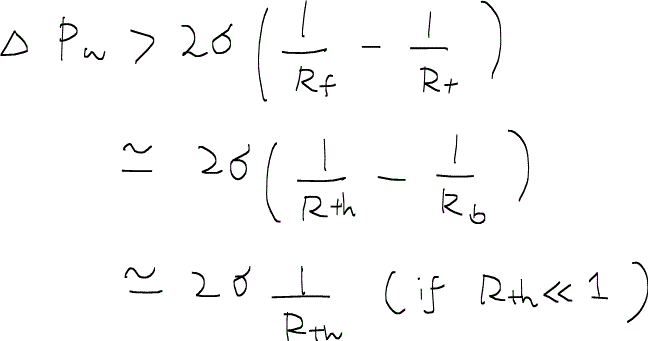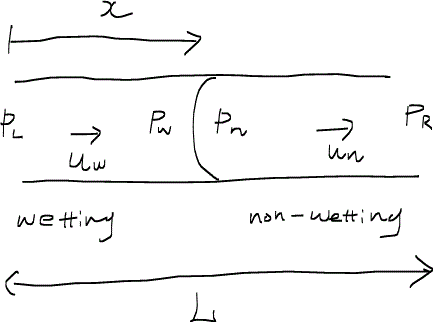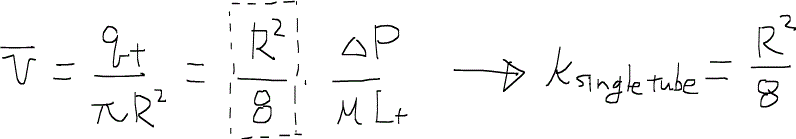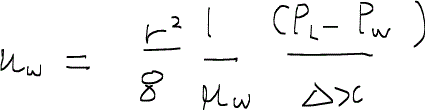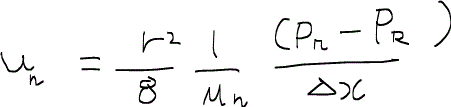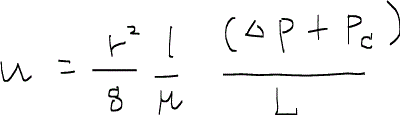油で満たされた水濡れ性の毛細管に水を通すと、壁際を水が選択的に流れるようになり孔隙の中心に油が取り残されるようになる。これをスナップオフsnap-offと言う。なぜこのようなことが起こるのかと言えば、孔隙が単純なチューブ状ではなく流路の幅に変化があるからである。孔隙同士の連結部で流路が狭い場所があると、水の流れが支配的になってゆく段階で図のように油相の一部が十分薄くなる。すると、ひょうたんのような形になった油はエネルギー的に切り離されて存在した方が安定するようになり独立した油の塊ができるのである。流れと切り離された非濡れ相(油)はもはや動くことができなくなり、いわゆるトラップされた状態に陥る。
ただし、一度スナップオフした油でも、より速い流速の水によって押し出すことができる。つまり、このようなトラップは流速に依存する現象rate-dependent phenomenonであると言える。
そこで次にスナップオフが生じた油を押し出す条件を、簡単なモデルを用いて整理してみたいと思う。
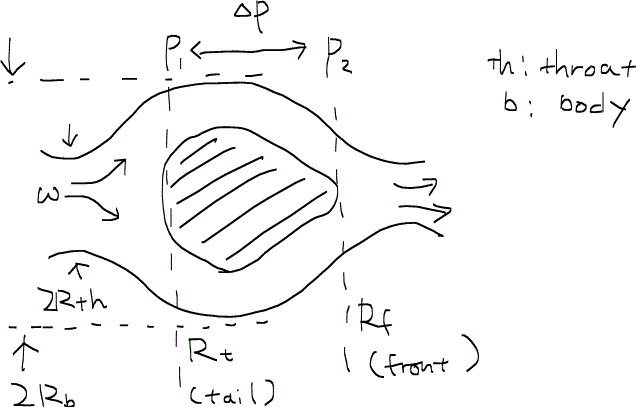
上の図は濡れ相に浸潤されている孔隙内に非濡れ相がトラップされている状態をモデル化した図である。非濡れ相は孔隙の中央に位置しており、孔隙の大きさは出入口部(throat)の直径が2Rth、本体部(body)の直径が2Rbで与えられているとする。また、非濡れ相は流れの先端部では半径Rf、後端部では半径Rtの塊を形成しているとしよう。
まず、ラプラス方程式より、先端部と後端部の毛細管圧力について次のような式ができる。
ただし、濡れ相の圧力差を
と定義した。なお、下付き字のwは濡れ相を、nwは非濡れ相を示しており、1および2は位置を示している。
いま、非濡れ相の先端部と後端部の圧力差を考えると、
となるが、
のときに、このトラップされた非濡れ相の塊を押し出すことができる。
つまり、この油がトラップを突破して流れることができるようになる条件は上の二式より、
となる。RthやRbが岩石固有の値であることを考えると、押している濡れ相の圧力差を強くかけるか、界面張力を下げれば油が流れ出すことが分かる。
また、もう一つ面白い表現方法としてはハーゲン・ポワズイユの式を用いるものが挙げられる。
ここで、ダルシー流速は、
と与えられているので、濡れ相と非濡れ相の流速はそれぞれ、
となる。ここで、流速と粘性が非濡れ相と濡れ相で等しいと仮定すると、
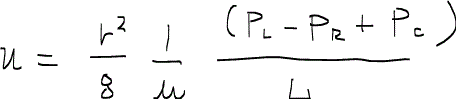
また、表現を簡単にするために、この区間での総圧力損失overall pressure dropを
と定義すると、
なる式が導かれる。すると、次のようなことが言えるようになる。
- Δp > 0のとき
外から圧力を加えている場合に相当し、分母は正の値なので濡れ相によって非濡れ相が圧力差を利用して掃攻されている状態 = force imbibition - Δp = 0のとき
外から何も圧力を加えていない場合に相当するが(コアの両端の圧力が同じ場合など)、分母はまだ正の値を持っているので、自発的に濡れ相が毛細管を進んでいく状態 = spontaneous imbibition - Δp + pc = 0のとき
反対方向から圧力を加えている場合(Δp < 0)に相当し、自発的な浸潤過程を無理やり止めている状態