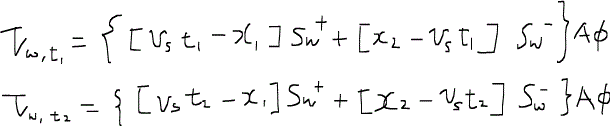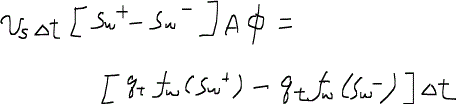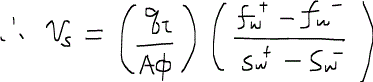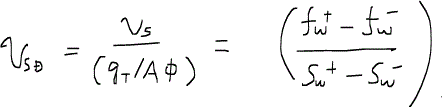単純な微分の計算では表現することができないショックフロントを生じさせるの物理的な制約を課す。それは、ある一つの仮定であり、「置換の速度は上流方向に単調減少する」というものである。つまり、フロント部分の速度が最も速く、それよりも上流(つまり圧入井側)ではフロントと同じか遅い置換速度でなければならない。この仮定は速度律velocity ruleと呼ばれている。
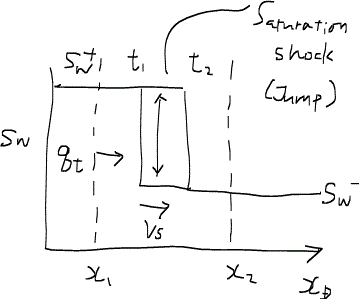
もしショックフロントが生じるとすれば、次のようにモデル化することができる。左から右に向かって水攻していると仮定してほしい。なお、vsはショックフロントの速度とした。
さて時刻t1、t2における水の体積はそれぞれ次のように与えられる。
したがって、t1からt2の間に増えた水の体積は、
一方で、フラクショナルフロー関数を用いると、次の保存式が得られる。
これらの方程式は等しくなければならないので、結局以下のような式展開ができる。
いままで考えていたように、時間と距離を無次元化すると、ショックフロントの無次元速度は、
となる。
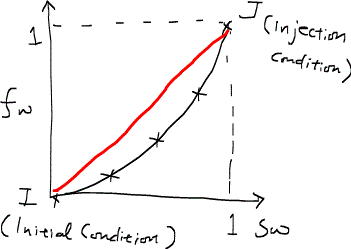
例えば、下図の黒実線で示されるようなフラクショナルフロー曲線を与え、水攻を実施した場合は、すべての飽和率領域で速度律違反になる。その結果、ショックフロントが生成されるわけだが、その(無次元)速度は赤線で描いたような弦chordの傾きに等しくなる。
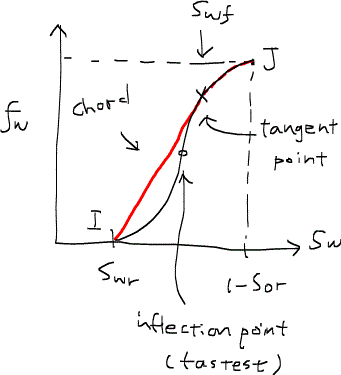
次に現実的なS型フラクショナルフロー曲線を与えてみるとどうだろうか。
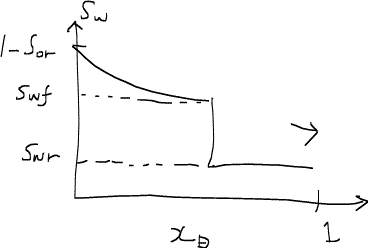
この場合は、まず初期条件Iからフラクショナルフロー曲線に向けて接線を引く。これまでの議論より接点tangent pointの飽和率がショックフロントの飽和率であることが分かる。この領域より下流は置換がまったく進んでおらず、初期の飽和率のままであるが、ショックが到達した瞬間に水の飽和率が0からSwfまで跳ね上がる。この点より上流(つまりSwf~Jの領域)には速度律に違反する部分が存在しないため、連続的に飽和率が変化する希薄波rarefaction waveとなるため、ショックが訪れた後は緩やかかつ連続的に水飽和率が上昇することが分かる。
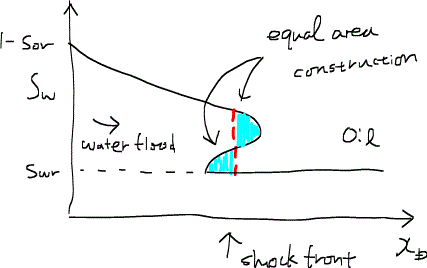
ここまで紹介した一次元の置換問題をフラクショナルフロー曲線と速度の関係から解く方法は、バックレイ・レバレットの解法Buckley-Leverett solutionと呼ばれている。最初にバックレイ・レバレット法が提唱された時、非物理的なフロント形状を、流体の体積に齟齬が生じないように図形的に処理してショックフロントの位置を計算していた。(下図参照)
しかし、のちにウェルジWelgeの論文で、ショックフロントの飽和率は速度律に基づいた接点の座標から与えられることが示され、図中の水色で塗りつぶした部分の面積を求めるための複雑な積分計算をする必要がなくなった。ウェルジはかの有名なフォン・ノイマンのアドバイスにより純粋な図形的解法を構築したと伝わっている。