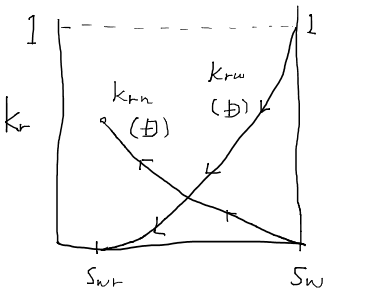
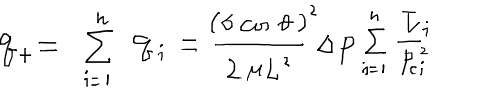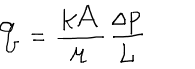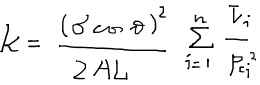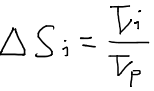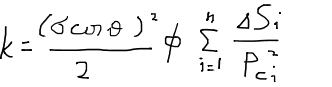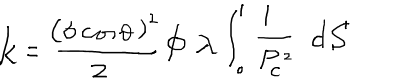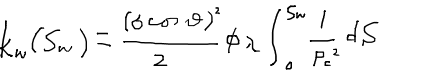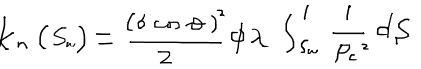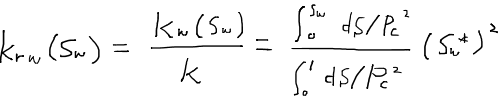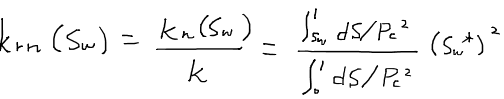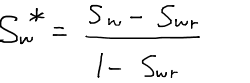相対浸透率と毛細管圧力の間には密接な関係がある。同じ現象を別の見方をしていると言っても過言ではない。これらの量はチューブ束モデルbundle of tubes modelによって結びつけることができ、一見定性的な量である相対浸透率を毛細管圧力によって表すことが可能である。まず、多孔質媒体を様々な太さを持つチューブだと仮定する。(チューブ束モデルbundle of tubes model)このときチューブ一本あたりの流量は次のように与えられる。
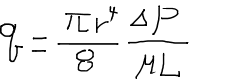
チューブ一本当たりの体積は長さと半径が分かっている場合
![]()
と与えられるので、結局
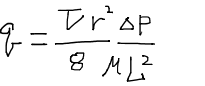
となる。これまでの議論で毛細管圧力が
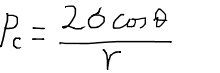
と表されることが分かっており、チューブ径の代わりに毛細管圧力によってチューブ一本あたりの流量を表現することが可能である。
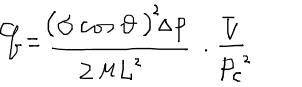
さて、今多孔質媒体は様々な径を持つチューブの集合であると仮定していることを思い出すと、媒体を通過する流体の全流量は単純に一本あたりの流量を合計すればよい。
さて、ここでの流量はダルシーの式
によっても表現でき、それを代入するとうまい具合に粘性が消えてくれる。
さらに右辺の体積Viが邪魔なので、孔隙体積の定義式である
とチューブiの飽和率への貢献度を表す
を用いると次の式が得られる。
この式は毛細管圧力と浸透率を結び付けるものであり、パーセルの方程式Purcell’s equationと呼ばれている。もし、チューブ径の分布が非常に滑らかならば積分による表現を使うことができる。
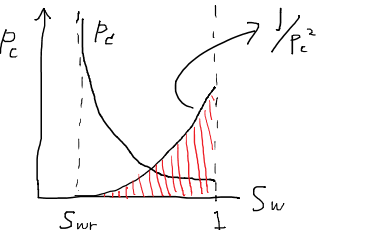
ただし、λはリソロジーファクターlithology factorと呼ばれる岩石固有の定数である。毛細管圧力曲線は飽和率の関数として与えられるため、積分項の計算は容易である。図形的には以下の図における斜線部の面積を求める演算となる。
飽和率を0から1までの範囲ですべて積分する代わりに、0から途中の飽和率Swで積分を行うと濡れ相の有効浸透率を得ることができる。残りの領域は非濡れ相が流れている分なので、非濡れ相の有効浸透率は範囲Swから1まで同じ式を積分して求めることができる。つまり、濡れ相、非濡れ相それぞれについての有効浸透率kw、knは次のように求めることができる。
ここで相対浸透率の定義を思い出すと、相対浸透率は有効浸透率を絶対浸透率で除したものであった。したがって、毛細管圧力曲線が分かれば相対浸透率を求めることができることが分かる。
ただし、Sw*は正規化した飽和率であり、これを乗じている理由は屈曲度を考慮するための補正である。
この屈曲度による補正を施した相対浸透率の導出方法はバーディンの理論Burdine’s theoryと呼ばれている。積分計算はパーセルの方程式と同じである。
ここで得られる曲線はトラップされる非濡れ相(油)が考慮されていない。すなわち、排出過程drainage processをモデル化している。非濡れ相の一部がトラップされる浸潤過程imbibition processの相対浸透率の求め方は次の記事でまとめる。