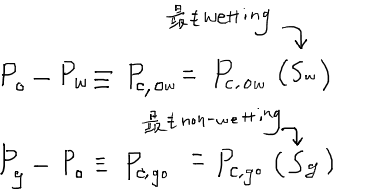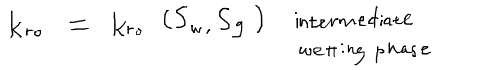三相流、すなわち水、油、ガス相が同時に存在するときの相対浸透率を考えるにあたって、まず各相の特性から整理したい。岩石は水濡れ性と仮定する。
- 水相:強い濡れ性(なるべく壁側にいたい)
- ガス相:強い非濡れ性(孔隙の中心にいたい)
- 油相:中間濡れ性(サンドイッチ状態)
つまり最も乾いているガス相が岩石表面と相性が悪く、最も濡れている水相が岩石表面と相性が良いと言える。油は水とガスの中間的な性質である。
さてここで、毛細管圧力が次のように与えられると仮定する。三相系における毛細管圧力の挙動はいまだ完全に解明されていないため、これらは仮定に過ぎないことに注意したい。
これらの式が意味しているのは、毛細管圧力が水(最も濡れ性の高い流体)の飽和率、もしくはガス(最も濡れ性の低い流体)の飽和率の関数として表されるということである。つまり中間濡れ性の流体の関数とは考えない。この仮定はレバレット仮定Leverett assumptionと呼ばれており、三相流の相対浸透率を考えるときのほぼ唯一の拠り所となる。
仮に毛細管圧力がレバレット仮定に従っているとすれば、三相系の相対浸透率は次のような関数として与えられるはずである。
ただし、krwは水相(濡れ相)相対浸透率、krgはガス相(非濡れ相)相対浸透率、kroは油相(中間濡れ相)相対浸透率である。
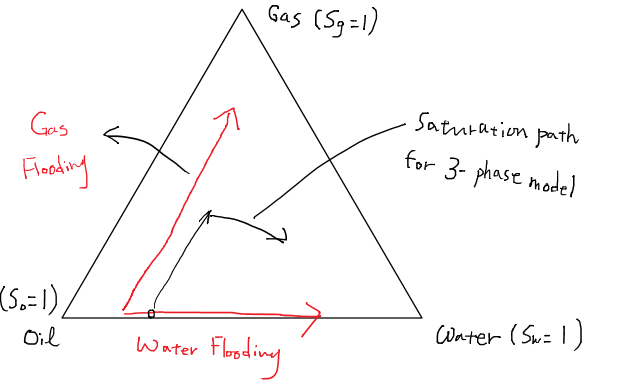
水とガスの相対浸透率はそれぞれ自分自身の飽和率のみの関数と仮定されており、二相系の実験のみから求めることができる。問題は油の相対浸透率であるが、これは二相系の実験をガス圧入、水圧入それぞれで実施し、それらの結果を内挿することによって表現している。なお、このときの実験の一方は排出過程となり、もう一方は必ず浸潤過程となる。内挿モデルとしてはStone I(1970)、Stone II(1973)、Baker(1988)などが経験的に提唱されている。導出された三相の相対浸透率が、二相系の実験によって得られた飽和率の軌跡saturation pathをよく再現していれば、内挿がうまくいっているとみなすことができる。適切な内挿モデルを使うことが大切であり、再現性について常に気を付ける必要がある。