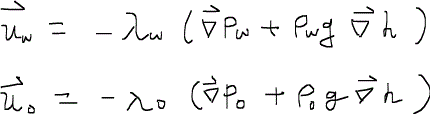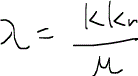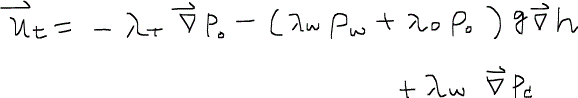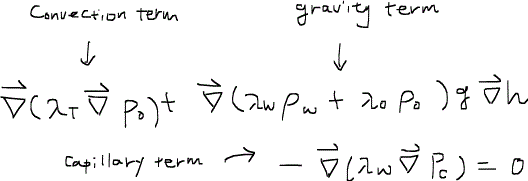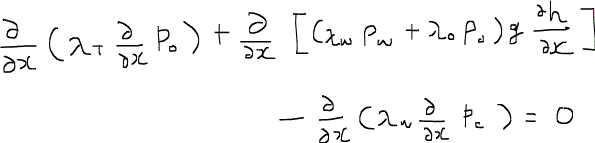これまで求めた式には流速uがそのまま入っていたが、ダルシーの法則を用いるとさらに式を具体化することができる。水と油の流速はそれぞれダルシーの式より次のように与えられる。
（14）
右辺は重力による移流項が含まれており、ρは流体の密度、gは重力加速度である。また、λは各相の易動度mobilityである。
（15）
ここでは、毛細管圧力が働いていることを仮定するため、油と水の圧力が異なっており、それらは次の式で結び付けられている。
（16）
毛細管圧力についてはすでに別途詳しくまとめたためそちらを参照のこと。さて、この式を使うと、水についての流速の式を次のように書き直すことができる。
（17）
このようにして求められた水と油の流速の式を足し合わせて、全流速を求めてみる。
（18）
ただし、λtは全易動度total mobilityを表し、
（19）
で定義される。
さて、ここでの全流速を（13）式に代入すると次の式が得れる。
（20）
移流項convection termは圧力差により生じる流れを、重力項gravity termは重力による鉛直方向の流れを、毛細管力項capillary termは毛細管圧力による流れを表している。この式は圧力方程式pressure equationである。つまりこれを解けば、任意の時間、場所の圧力を求めることができる。
一次元の流動を考えると、上の式は次のように具体化される。
（21）
