それでは早速ルジャンドル変換とはどういった手法なのか紹介しよう。ここで扱うルジャンドル変換Legendre transformation とは、全微分可能な二変数関数に対して、もともとの変数の代わりにそれらに関する偏微分係数を変数とする新たな関数を生成する変数変換の手法である。要するに![]() のような関数から、変数変換を経て
のような関数から、変数変換を経て ![]() や
や![]() 、もしくは
、もしくは![]() のような形の関数を生成しようという訳だ。
のような形の関数を生成しようという訳だ。
ある全微分可能な二変数関数![]() があったとき、その変数
があったとき、その変数![]() と
と![]() に関する偏微分係数をそれぞれ
に関する偏微分係数をそれぞれ
(61) ![]()
(62) ![]()
と書くとする。すなわち関数![]() の全微分は、
の全微分は、
(63) 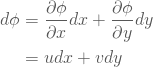
と表現できる。さてこのとき関数![]() を、変数
を、変数![]() と
と![]() のどちらか片方、または両方を
のどちらか片方、または両方を![]() ,
, ![]() で変数変換を行おうとすれば、
で変数変換を行おうとすれば、
(i) ![]() を
を![]() で変換する
で変換する
(ii) ![]() を
を![]() で変換する
で変換する
(iii) ![]() を
を![]() で変換し、
で変換し、![]() を
を![]() で変換する
で変換する
なる3 パターンが考えられる。
変数変換の結果、![]() の代わりに得られる新しい関数をそれぞれ(i)
の代わりに得られる新しい関数をそれぞれ(i) ![]() 、(ii)
、(ii) ![]() 、(iii)
、(iii) ![]() と表すならば、それぞれの関数は以下のように定義すればよい。
と表すならば、それぞれの関数は以下のように定義すればよい。
(64) ![]()
(65) ![]()
(66) ![]()
このような形で新しい関数を生成することをルジャンドル変換と呼んでいる。上で定義した関数が、きちんと変数変換されているかどうかを以下で検証する。
(i) 関数![]() が
が![]() と
と![]() の関数になっているかの検証
の関数になっているかの検証
まず、(64)式の全微分を取ると、
(67) ![]()
となるが、ここで(63)式を適用すると、以下のように式を整理することができ、変数![]() と
と![]() の関数になっていることが示せる。
の関数になっていることが示せる。
(68) ![]()
なお、これを![]() ,
, ![]() を独立変数とする関数
を独立変数とする関数![]() の全微分
の全微分
(69) ![]()
と比較すると、以下のような関係が成り立っていなければならないことが分かる。
(70) ![]()
(71) ![]()
(ii) 関数![]() が
が![]() と
と![]() の関数になっているかの検証
の関数になっているかの検証
同様に、関数![]() の全微分を取ると、
の全微分を取ると、
(72) ![]()
となり、関数![]() もやはり変数
もやはり変数![]() と
と![]() の関数になっていることが分かる。
の関数になっていることが分かる。
また、こちらも同様に、![]() ,
, ![]() を独立変数とする関数
を独立変数とする関数![]() の全微分
の全微分
(73) ![]()
と比較すると、以下のような関係が成り立っていなければならない。
(74) ![]()
(75) ![]()
(iii) 関数![]() が
が![]() と
と![]() の関数になっているかの検証
の関数になっているかの検証
同様に、関数![]() の全微分を取ると、
の全微分を取ると、
(76) ![]()
となり、関数![]() もやはり変数
もやはり変数![]() と
と![]() の関数になっていることが示された。
の関数になっていることが示された。
また、こちらも同様に、![]() ,
, ![]() を独立変数とする関数
を独立変数とする関数![]() の全微分
の全微分
(77) ![]()
と比較すると、以下のような関係が成り立っていなければならない。
(78) ![]()
(79) ![]()
以上をまとめると、結局次の表のようになることが分かる。
表3. 一般的なルジャンドル変換の対応表
| 変数 | ||||
| 関数形 | ||||
| 変数変換 | ||||
| 変換式 | ||||
| 全微分 | ||||
| 拘束式 |








