各相における成分iのモル分率を示す![]() 、
、![]() を求めるにはまず気相と液相のモル分率を示す
を求めるにはまず気相と液相のモル分率を示す![]() と
と![]() を導出しなければならない。実はすでにその道筋は示されていて、成分
を導出しなければならない。実はすでにその道筋は示されていて、成分![]() についての平衡定数
についての平衡定数![]() が求っていれば、平衡定数の定義より気相のモル分率を示す
が求っていれば、平衡定数の定義より気相のモル分率を示す![]() を計算することができる。式の対照性より
を計算することができる。式の対照性より![]() の代わり
の代わり![]() を先に求めてもよいが、ここでは
を先に求めてもよいが、ここでは![]() を求めることにする。まず、(61)式でも示されているとおり、
を求めることにする。まず、(61)式でも示されているとおり、
(68) 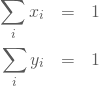
なので、それぞれを比較すると次の式を得ることができる。
(69) ![]()
また、上式の左辺は、(63)、(64)式より、
(70) 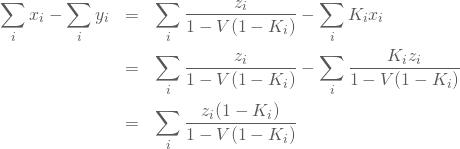
のように書くことができ、(69)式と組み合わせると以下のようなVについての方程式が導ける。
(71) ![]()
求められた式を見ると、![]() はフィードとして与えられており、
はフィードとして与えられており、![]() は求めたばかりなので、結局
は求めたばかりなので、結局![]() 一変数のみについての方程式となっていることが分かる。さてここで、関数
一変数のみについての方程式となっていることが分かる。さてここで、関数![]() を
を
(72) ![]()
のように定義すると、
(73) ![]()
なる方程式の解が求める![]() ということになる。この方程式はラッシュフォード・ライス方程式Rachford-Rice equationと呼ばれることがある。ラッシュフォード・ライス方程式を解くには、二分法bisection methodがまずは用いられる。(一次元の)ニュートン・ラフソン法を使って数値的に解く手法や、二分法とニュートン・ラフソン法を組み合わせた混合ニュートン二分法mixed Newton-bisection methodも用いられる。ニュートン・ラフソン法によって方程式を解く際には(72)式の一次導関数が必要なのでここで示しておく。
ということになる。この方程式はラッシュフォード・ライス方程式Rachford-Rice equationと呼ばれることがある。ラッシュフォード・ライス方程式を解くには、二分法bisection methodがまずは用いられる。(一次元の)ニュートン・ラフソン法を使って数値的に解く手法や、二分法とニュートン・ラフソン法を組み合わせた混合ニュートン二分法mixed Newton-bisection methodも用いられる。ニュートン・ラフソン法によって方程式を解く際には(72)式の一次導関数が必要なのでここで示しておく。
(74) ![]()
計算された![]() の値を(63)、(64)式にすでに求められている
の値を(63)、(64)式にすでに求められている![]() および
および![]() とともに代入するとそれぞれ
とともに代入するとそれぞれ![]() 、
、![]() の値を得ることができる。なお、
の値を得ることができる。なお、![]() が極めて小さくなると思われる場合は、
が極めて小さくなると思われる場合は、![]() の代わりに
の代わりに![]() について解けばよく、その場合ラッシュフォード・ライス方程式は、
について解けばよく、その場合ラッシュフォード・ライス方程式は、
(75) ![]()
となる。また、その一次導関数は、
(76) ![]()
である。








