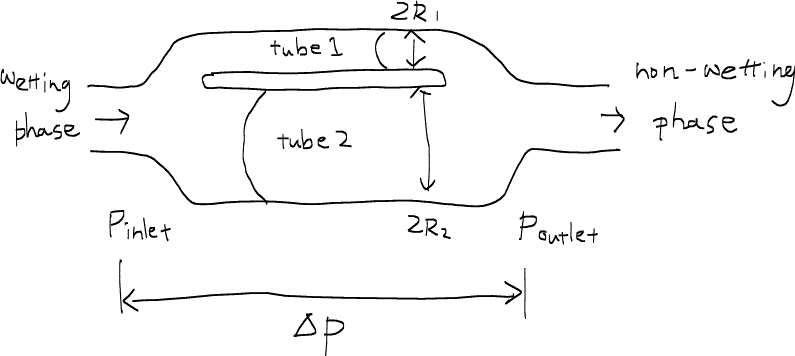
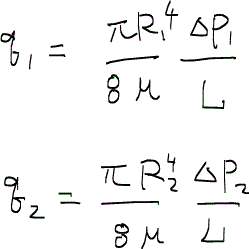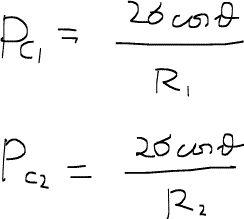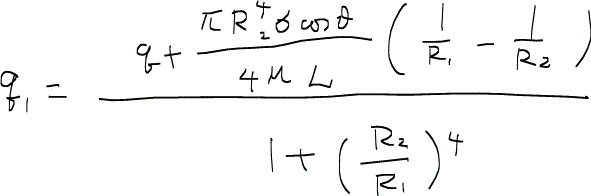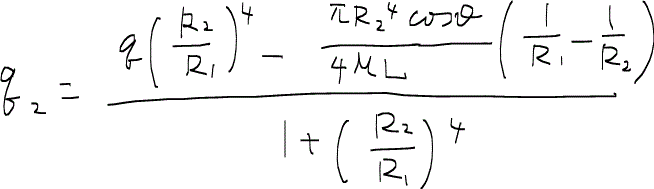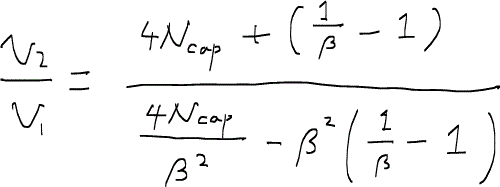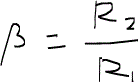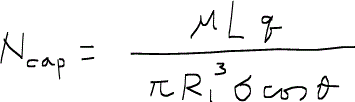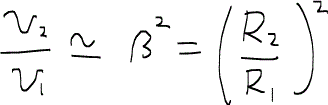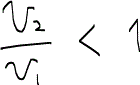孔隙二重管(ポアダブレットpore doublet model)モデルはバイパス化bypassingを観察しモデル化するためにされた実験である。バイパス化とは、濡れ相流体が小さな孔隙径を持つ毛細管ばかりを流れてしまい、非濡れ相流体が大きな孔隙径を持つ毛細管内にトラップされてしまうことを言う。
ここでは、孔隙二重管モデルの実験を元にバイパス化がどのような要素によって引き起こされるのかを定量的にモデル化する。まず孔隙二重管とは径の異なる二本の毛細管をつなぎ合わせた特殊な管である。細い方の毛細管の半径はR1とし、もう一方の太い毛細管の半径はR2とする。最初この管の中は非濡れ相で満たされており、そこを濡れ相流体で押してゆく。
さてここで、それぞれの管に対してハーゲン・ポワズイユの式を立てる。
ただし、二本の毛細管は出入口を共有しているので、二本の管は出口と入口の圧力差が同じでなければならない。つまり、
なる式が成り立つことが必要である。ここでのPc1は管1の毛細管圧力、Pc2は管2の毛細管圧力であり、次のように与えられている。
いま、全流量total flow rateなる量qを、
と定義し、ハーゲン・ポワズイユの式を整理すると次のような式が得られる。
ここで、平均流速(v = q/πr2)をそれぞれの管について計算し、その比を取ってみる。
ただし、βは不均一性係数heterogeneity factorと呼ばれる係数で、
として与えられ、Ncapは毛管値またはキャピラリー数capillary numberと呼ばれる係数で次のように与えられる。
ここで、流速が大きいときには、キャピラリー数が無限大と見なすことができるので、
となり、R2 > R1であったことを思い出すと管1の油が取り残されることになる。これは、毛細管力と粘性力がせめぎ合った結果、粘性力が勝った状態と解釈できる。一方流速が小さいと、
となり、今度は系の大きな管2に油が取り残される。これは毛細管力が卓越している状態と言える。流速や径の値に現実的なものを与えるとこの条件になることが多いため、バイパス化のモデルと言われる。
なお、キャピラリー数による場合分けでも分かるとおり、キャピラリー数が増えていくと粘性力が毛細管力に勝るようになり、トラップ現象が起きづらくなる。また、もし管の径がどこでも均一になるような、局所的な不均質性が存在しない場合はトラップは発生しない点にも注意されたい。
まとめると、結局のところ孔隙二重管の挙動は管の大きさ(径)とキャピラリー数によって決まる。つまり、バイパス化は孔隙径の分布とキャピラリー数に依存していると言える。ただし、実際に孔隙二重管の実験を行ってみると粘性力と毛細管力のバランスが難しく、適切な結果を得ることが難しいことが分かっている。つまり孔隙二重管モデルは一種の概念モデルconceptual modelである訳だが、バイパス化がどのようなパラメータに依存するかについての示唆を与えてくれるという点で有意義である。