now♯

half tone higher than now

実在気体の化学ポテンシャル

理想気体の代わりに実在気体を考えるには、分子間力と分子自身の大きさの影響により圧力を補正する必要がある。しかし実在気体の分子間力や分子自身の大きさは、当然分子種ごとに異なり、一般化した数式で表すことが難しい。そこで実在気体の状態方程式に倣って一計を案じる。実在気体の状態方程式では、

(133)   \begin{equation*} \begin{split} pV=znRT \end{split} \end{equation*}

のようにzファクターを定義して圧力のずれを補正したが、実在気体の化学ポテンシャルを求めるときも、理想気体の化学ポテンシャルを表す(132)式中の圧力pの代わりに、非理想性による影響を織り込んだ実効圧力のようなものを考える。このときの実効圧力のようなもののことをフュガシティfugacityと呼び、記号fを与える。すなわち、理想気体の化学ポテンシャルはフュガシティを用いて次のような式で表すことができる。

(134)   \begin{equation*} \begin{split} \mu=\mu_0+RT\ln\left(\frac{f}{p_0}\right) \end{split} \end{equation*}

もしくは、

(135)   \begin{equation*} \begin{split} d\mu=RTd\ln{f} \end{split} \end{equation*}

なお、(134)式で、右辺第二項の分母がf_0ではなく、p_0になっているのは、十分低圧な領域であれば実在気体は理想気体と見なせるからである。すでに書いたとおり通常p_0は大気圧をとるので、f_0 =p_0と見なせるという訳である。

このあたりの性質は次のような図を見ると分かりやすいだろう。

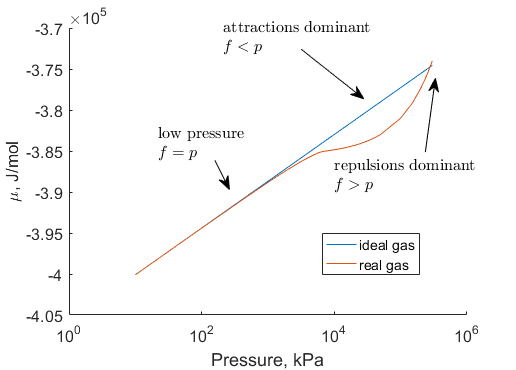
図6 実在気体(CO2)の化学ポテンシャル

まず、圧力が低くなるにつれて、理想気体と実在気体の化学ポテンシャルは漸近する。これは低圧領域では分子同士が十分離れており、分子間力の影響が無視できるようになるからである。逆に圧力が高くなっていくと徐々に分子間力の影響が無視できなくなり、理想気体と実在気体の化学ポテンシャルが乖離するようになる。実在気体では分子間力による引力が働くので

実在気体のフュガシティ ＜ 理想気体の圧力

になるので、化学ポテンシャルについても

実在気体の化学ポテンシャル ＜ 理想気体の化学ポテンシャル

という関係になる。（図中のAttractions dominantと書かれている領域）

しかし徐々に高圧にしていくと、またその差がなくなってゆく。これは圧力が高くなると、分子同士が近づきすぎて分子自身の大きさにより反発する力（斥力）が働き、分子間力による引力を相殺するためである。さらに高圧の領域になると斥力のほうが強く作用するようになるので、

実在気体のフュガシティ ＞ 理想気体の圧力

すなわち、

実在気体の化学ポテンシャル ＞ 理想気体の化学ポテンシャル

という関係になり、理想性が失われてゆく様子が分かる。（図中のRepulsions dominantと書かれている領域）