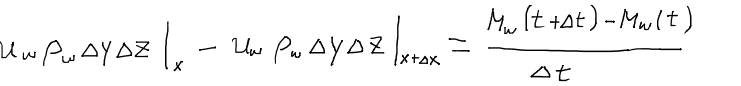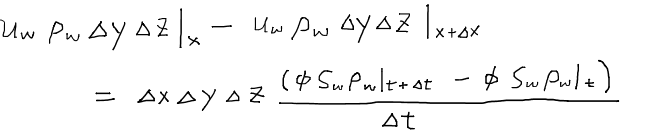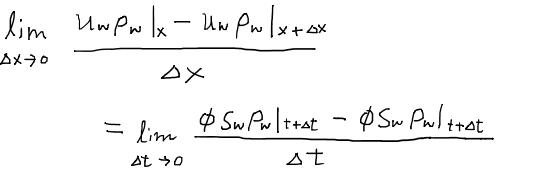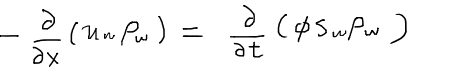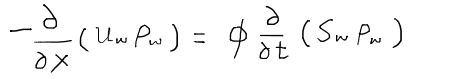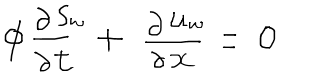ここからは流動方程式flow equationを組み立てて、一次元の置換問題1D displacement problemを考えていく。置換とは例えば油で満たされた媒体に水を圧入して油を回収する過程のことを言う。まずはこのような問題を簡単に解くために、圧入流体と置換流体が互いに混和しない非ミシブル状態immiscible stateを仮定する。圧入流体と置換流体が一つの相になって流れるミシブル状態miscible stateの置換問題は熱力学的な相平衡を考慮する必要があるため、別の場所で解説することとする。
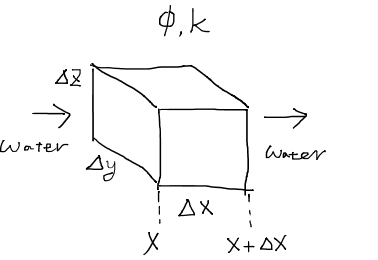
さて、流動方程式を立てるには、まず以下のような領域を定義してその質量保存を考えることから始める。
領域を直方体として表現すると、ここに存在する水の質量は、
と書くことができる。ただし、φは孔隙率、Swは水の飽和率、ρwは水の密度を表す。
ここで、ダルシー流速(体積流量volumetric flow rate)であるuwを用いると、質量流量mass flow rateはuwρwと表される。なお質量流量とは、単位時間・単位断面積あたりにその面を通過する流体の質量のことである。さて役者がそろったので早速質量保存の式を考えてみると次のようになる。
左辺の各項は断面積ΔyΔzの壁を通り抜ける単位時間あたりの水の質量を表しており、右辺は水の質量の増減を表している。つまり、左の壁から入ってきた量から右の壁へ出ていった量の差引が、この領域に蓄えられた水の量となることを示しており、典型的な質量保存の式となっている。なお、右辺は最初の式を用いると書き直すことができる。
この式の両辺をΔxΔyΔzで割ってΔx→0の極限を取ると次の式になる。
これは偏微分の表現に他ならないので、偏微分記号を用いて結局次のように表現される。
この式こそが1次元における水の質量保存の式である。もし、岩石が非圧縮incompressibleだと仮定できる場合、つまりφ=const.のときは、
と書ける。また水も岩石も非圧縮だと仮定できる場合、すなわちφ=ρw=const.のときは、両辺から水の密度をキャンセルアウトすることができ、次のような簡素な形の式が得られる。