濡れ相(水)による非濡れ相(油)を置換している際に生じるトラップのメカニズムについて論じるために、毛細管圧力曲線をもう少し観察してみる。あるコアの排出過程と浸潤過程の毛細管圧力をプロットしたときに次のような曲線が得られたとする。
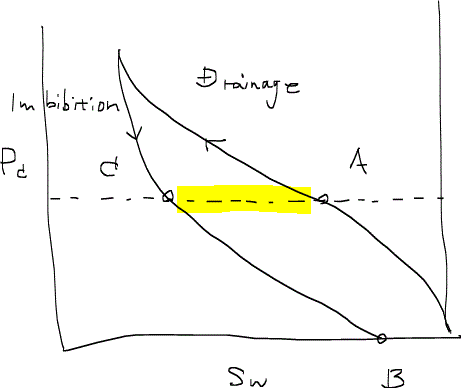
このとき、点Aと点Cは同じ毛細管圧力を共有しており、これはつながっている非濡れ相の形状が同じ状態にあることを示している。つまり、流れている非濡れ相が存在している場所が点Aと点Cでは黄色い部分で同じなのである。
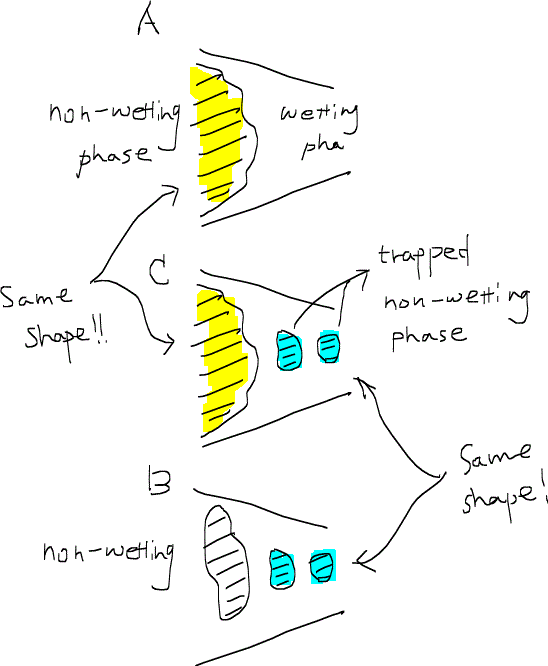
また、点Cから浸潤過程をさらに進めると完全に非濡れ相がトラップされている点Bに至るが、点Cの時点ですでにトラップされていた非濡れ相の形は変わらない。青く塗った部分である。
ここで、ふと点Aから浸潤過程に入ったら、どのくらいの非濡れ相がトラップされるかを予測してみたいと思う。というのも、上のような関係を用いると簡単な飽和率同士の差引で求めることができるからである。つまり、次のように空間的な差引で、点Aから浸潤過程を行った場合の残留油量は次のような関係によって求めることができる。
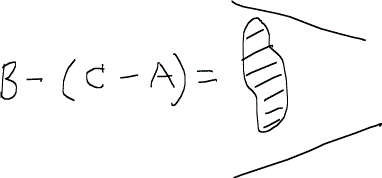
これはつまり、ある非濡れ相飽和率を初期に持つ油層やガス層に水攻を施したらどのくらいの油ガスがトラップされるかを示唆しているので、技術的に大変意義深い。
このあたりの考察を実験をもとに調べたのがランドで大変便利な式を残した。今、下のような毛細管圧力曲線が得られていたとする。黒実線が排出過程、赤実線が浸潤過程である。この油層が初期油飽和率Snwiを持っていると仮定した場合の残留油飽和率Snwrを予測する。つまり、初期の状態が点Aで、点A’に向けて浸潤過程を実施することを想定する。
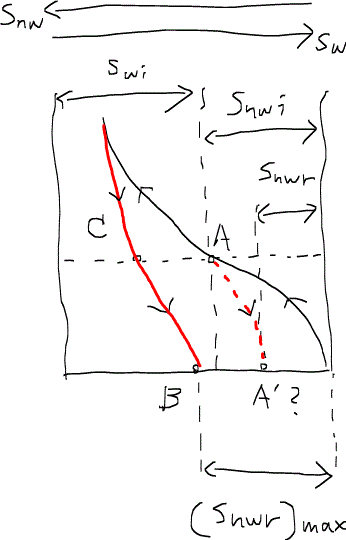
Snwi、Snwrについては、次のような正規化した飽和率を得ることができる。
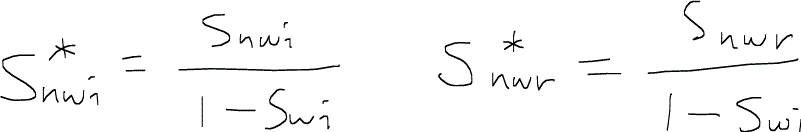
ここでの*印は初期の非濡れ相飽和率(1 – Swi)で正規化normalizeした飽和率であることを示している。つまり、Snwi*は常に1になるようになっている。これらの値を用いると、実験的に次のような関係が常に成り立つことが分かっている。
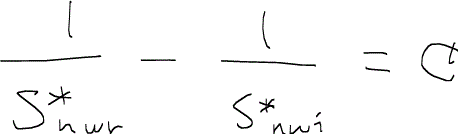
ただし、Cは定数であり、ランドの定数Land’s trapping coefficientと呼ばれる。
ここでもし、非濡れ相の残留飽和率に(Snwr)maxを使うと、結局次のような関係が得られる。
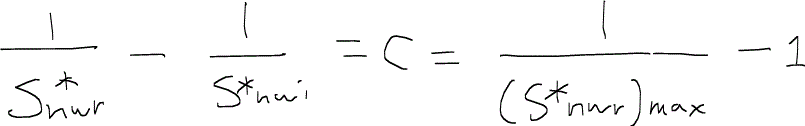
なお、
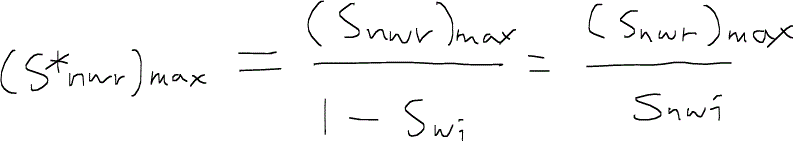
である。すなわち、もしCが与えられているのならば、初期の非濡れ相飽和率に応じてSnwrまたは(Snwr)max をいつでも予測することができ、トラップされる非濡れ相について定量的に考察することが可能となる。








