熱力学的に平衡条件が満たされていることを保証するには、各相のフュガシティが等しいことを示せばよいのであった。しかし、肝心のフュガシティはどのように計算すればよいのだろうか? 実は熱力学だけではその先に進むことができないので、状態方程式と組み合わせることでフュガシティを計算する式を導き出す。すなわち、熱力学の理論的な世界と状態方程式の実用的な世界がここで始めて繋がるのである。
それでは、実際に観測できる量を駆使してなんとかフュガシティを定式化してみることにしよう。簡単のために単成分系(純物質)を考えることにする。まずフュガシティを定義している式である、
(1) ![]()
なる式では、化学ポテンシャルの項が計算しにくいのでこれを消去することを考える。すでに何度も登場したように、前章の表4よりギブズエネルギーの微分は
(2) ![]()
のように与えられているが、前提条件として温度と粒子数が一定であるとすれば、次のように簡略化することができる。
(3) ![]()
この式を物質量![]() で割ると化学ポテンシャルについての次の関係を得ることができる。
で割ると化学ポテンシャルについての次の関係を得ることができる。
(4) ![]()
ただし、![]() はモル体積molar volumeである。次に(1)式と(4)式を組み合わせて化学ポテンシャルを消去すると、次に示すようにだんだんと計算できそうな方程式になってくる。
はモル体積molar volumeである。次に(1)式と(4)式を組み合わせて化学ポテンシャルを消去すると、次に示すようにだんだんと計算できそうな方程式になってくる。
(5) ![]()
しかし、まだ微分形式なのが鬱陶しいので何とかしようと思う。とりあえず、フュガシティは圧力![]() とフュガシティ係数
とフュガシティ係数![]() を用いて、
を用いて、
(6) ![]()
と書けるので(5)式は次に示すように変形してゆくことができる。
(7) 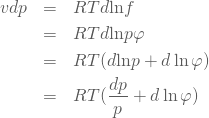
そしてこの式の形を少々整えると次のようになる。
(8) ![]()
この形まで導くことができれば、定積分をある基準圧力![]() とそのときのフュガシティ係数
とそのときのフュガシティ係数![]() の状態から、任意圧力
の状態から、任意圧力![]() とそのときのフュガシティ係数
とそのときのフュガシティ係数![]() までの区間で行って、微小変化量の項を消すことができる。
までの区間で行って、微小変化量の項を消すことができる。
(9) ![]()
積分項の一部は計算することができて次のように式展開できる。
(10) 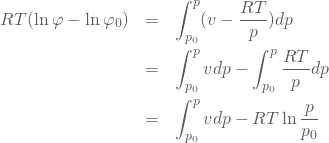
さて、微分が消えたのはよいが、今度は積分項がやや計算しにくいので積分変数の変換を試みる。と言っても対処法は実に簡単で、以下に示すように![]() の全微分を考えればよい。
の全微分を考えればよい。
(11) ![]()
分かりやすいように移項しておく。
(12) ![]()
この式を![]() から
から![]() 、
、![]() から
から![]() の区間で積分すると次の式が得られる。
の区間で積分すると次の式が得られる。
(13) 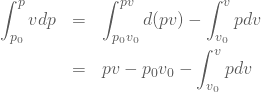
今、(10)式の積分変数を変換したいと思っていたので、そこに(13)式を代入すると次の式を得ることができる。
(14) ![]()
積分の計算を工夫するために、この式に若干トリッキーな変形を施すと以下の式が導かれる。
(15) ![]()
定積分の項の一部が計算できるのでさらに頑張って変形してみる。
(16) 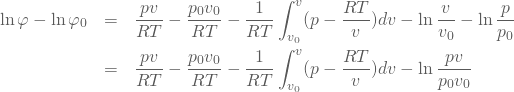
また、実在気体の状態方程式、
(17) ![]()
を使えば、zファクターを用いてもう少しだけ式を簡単にすることができる。ただし![]() は
は![]() 、
、![]() におけるzファクターを示すこととする。
におけるzファクターを示すこととする。
(18) ![]()
ここで、計算の基準となる点の条件として![]() を仮定してみる。まず、zファクターについて計算すると、
を仮定してみる。まず、zファクターについて計算すると、![]() の極限ではあらゆる気体は理想気体と見なすことができるので、
の極限ではあらゆる気体は理想気体と見なすことができるので、
(19) ![]()
である。次に![]() のときにフュガシティ係数が1になることは前章(138)式で示されている。つまり、
のときにフュガシティ係数が1になることは前章(138)式で示されている。つまり、
(20) ![]()
であるので、結局
(21) ![]()
となることが分かる。また状態方程式を見れば自明であるが、![]() と
と![]() が一定であれば、
が一定であれば、![]() で
で![]() になるため、
になるため、
(22) ![]()
も使うことができる。したがって、![]() とすれば(18)式は最終的に次のような形に帰着する。
とすれば(18)式は最終的に次のような形に帰着する。
(23) ![]()
なお、この式は体積についての積分が含まれているが、圧力表示pressure explicitの状態方程式をそのまま代入すると積分計算ができる形になっている。前の章で登場したさまざまな状態方程式を思い出すと分かると思うが、いずれも![]() という圧力に明示的explicitな式としてまとめられており、そのような状態方程式を(23)式に直接代入すると被積分関数を
という圧力に明示的explicitな式としてまとめられており、そのような状態方程式を(23)式に直接代入すると被積分関数を![]() の関数として表すことができる訳である。わざわざ煩雑な積分変数の変換を行なったのは、簡単にフュガシティを計算するための布石だったのだ。
の関数として表すことができる訳である。わざわざ煩雑な積分変数の変換を行なったのは、簡単にフュガシティを計算するための布石だったのだ。
なお、変数変換を行なう前の(10)式を整えると次のような式になる。こちらは体積表示volume explicitの状態方程式を代入するための形と言える。
(24) ![]()








