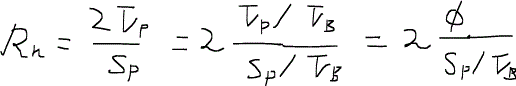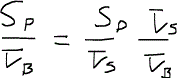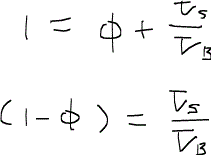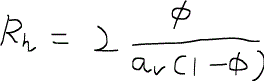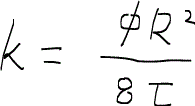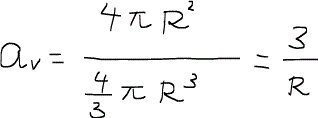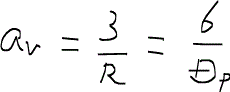これまでの議論によると浸透率はチューブの半径、孔隙率、屈曲度に依存することになっている。つまり、
である。孔隙率と直接関係があるので、相関式を考える時の根拠になる式である。ところで、浸透率に一番効いてくる変数は何かといえば、どうやらチューブの半径のようである。いままで考えていたモデルだと、円柱状のチューブを考えていたので単純だったが、より現実的なモデルにするにはREVの時に考えたように岩石基質が球でできていると仮定したい。そのために、水力半径hydraulic radiusなるものを導入する。
(2次元断面)
(3次元)
![]()
例えば、二次元断面で円柱状のチューブを考えると、水力半径は次のような演算により結局Rになる。
より誤解を生まないように一般的に記述するならば、孔隙体積と孔隙の表面積を用いて、
と書いておくこともできよう。
さて、ここで、右辺の分子、分母をバルク体積VBで割り算すると、次のような式が得られ、孔隙率と結びつけることができる。
さて、ここでもう少し頑張って、意味あり気な式を導いてみる。気に入らないのは右辺の分母であるが、孔隙率を使って変形を試みる。まず、
のように書ける。次にバルク体積は孔隙体積と岩石の粒子体積の和であるので、
であり、これを変形すると、
となる。これらの関係を用いると、
なる式が得られる。
ここで、比表面積のようなものが得られるので、avなる記号を与えてspecific surface areaと呼ぶ。
これを用いると、結局水力半径は
となり、すでに求めた
なる式のチューブ半径Rに水力半径を代入してみると次の式が得られる。
ここで岩石基質の粒子を球だと仮定すると、
となる。avは流体にさらされる表面積の大きさを表す指標であり、球の半径に反比例する。つまりコーヒー豆を細かく挽く(Rが小さくなると)とavは大きくなり、苦いコーヒーができるという訳。
なお、ここで半径の代わりに直径Dpを用いると、
となるので、これを用いると結局、
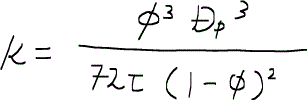
という形の浸透率についての方程式が得られる。この式こそがカルマン・コゼニー方程式Carman-Kozeny equationである。カルマン・コゼニー方程式は概念的な式であり、実際に浸透率を求めるのに使われることはまずないが、浸透率という量が何に依存するかを示しているという意味で大変重要である。