濡れ相で満たされた円錐型conicalの毛細管内に非濡れ相を押し込んでゆくことを考える。岩石は水濡れ性と考えることが多いので、ここでの例では水で満たされた円錐型の孔隙に油を押し込むことを考えたい。
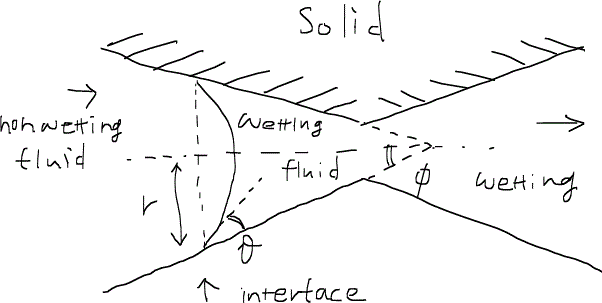
完全な円錐だと詰まってしまうので、ここでは円錐を二つくっつけたようなモデルにした。左から右に非濡れ相が侵入していると思ってほしい。接触角をθ、円錐を横から見た時の角度をφとすると、曲率半径は、
![]()
と書くことができる。つまり、先細りの孔隙にものを押し込むときは、その図形的な性質(つまりφ)に影響されることが分かる。
この式をラプラス方程式に代入すると、
![]()
なる式が得られる。ここでの下付き文字nwは非濡れ相nonwetting phase、wは濡れ相wetting phaseを示す。この式はいわゆる毛管バリアの存在を示唆しており、流体を押し込んでゆくと毛細管圧力の上昇によってどんどん入りにくくなることが分かる。しかし、押し込んだ非濡れ相流体は、流路が最も狭くなる地点を通過した瞬間に堰を切ったように流れ出す。これはヘインのジャンプHaine’s jumpと呼ばれる。
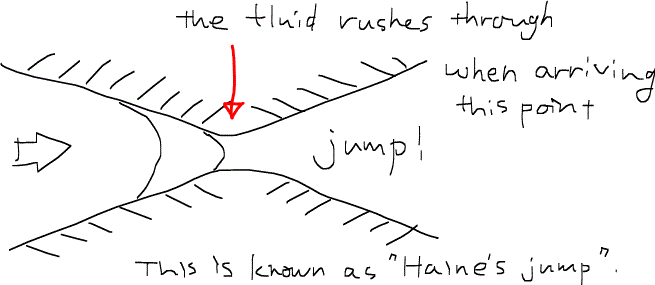
岩石に流体を押し込んだ時に、ある一定の圧力を超えるとその流体が通り抜け始めるがその圧力を、閾値圧(スレッショルド圧力threshold pressure)という。閾値圧はもっとも小さい孔隙の半径に依存することが分かる。すなわち、多孔質媒体中のでの流体の流れ方は、岩石や孔隙がどのように分布しているかに強く依存するのである。








