特に物理学ではそうなのだが、何か新しい理論を組み立てるときには、現象をモデル化するための大原則とも言える仮定postulateが必要である。物理学は自明の理をモデル化して、その数学的な展開によって組み立てられたものではなく、真偽はまだ分からないが仮にこのアイデアが正しいとすれば・・・、というような仮定が必要な場合がしばしばある。特に理論の前提となる仮定を公理axiomと呼ぶ。ひとつ注意しておくと、公理を定理や法則と混同してはならない。定理や法則というものは公理から導かれるべきものであり、公理は往々にしてそれ自身を導くことはできない。しかも公理は必ずしも自明でなくてもよい。ここでは熱力学の公理を紹介するが、それらは先験的a prioriに証明することができないものであることをまず記しておく。
あまり意識されていないことかもしれないが物理学は典型的に帰納的a posterioriなスタンスをとっている。つまり、物理学のアプローチとは、ある公理を定めて、数学的な展開を行い、定理や法則を導き出し、それが実際起こっている現象の観察と一致するかを確かめるというものである。熱力学でも公理から導かれる種々の結果と実験結果がよく一致することから、その公理の正当性が認められているのである。現在生き残っている物理学の理論は、現象を大きな矛盾なく説明できているというだけであり、矛盾が生じたときは公理の一部または全部に修正を加えたり、ひどい場合は理論自体が放棄されたりして発展してきた。なので、なぜこのような仮定を置くの? といった疑問に対する(投げやりだが)的を射た回答は、とりあえずうまくいっているから。である。
さて前置きが長くなったが、ここでようやくマクロ系の平衡状態を議論するときに設ける、3個の重要な仮定を紹介する。
- 熱力学的な系の平衡状態は、それぞれ示量性変数である内部エネルギーU、系の体積V、成分ごとの粒子数Nの関数として示されるエントロピーSによって完全に特徴付けられる
- U、V、Nを物理的に取りうる範囲でさまざまに変化させて得られるSのうち最大のものが平衡状態のエントロピーである
- エントロピーは相加的で連続的微分可能な関数であり、内部エネルギーUが増加するにつれて単調に増加する性質を持ち、その下限は
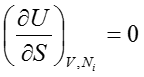
のときにとる0であり、上限はない
次にこれらの3個の仮定についてそれぞれ説明したい。








