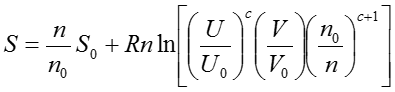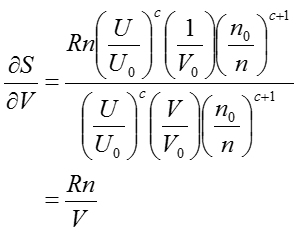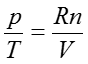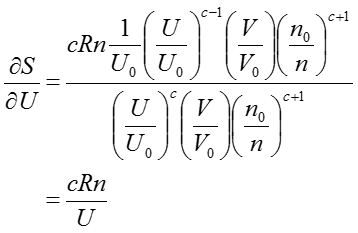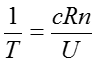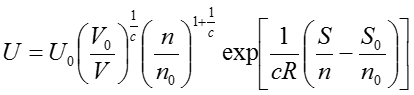気体のPVT関係を考えるには、古典的には気体の分子運動論という考え方を用いる。気体を閉じ込めている容器の壁にどのくらいの頻度で分子が衝突するかをモデル化するアプローチだ。そのとき、最も簡単なモデル化は、気体分子を質点と考え、それぞれの分子には相互作用がないものと仮定することである。つまり、気体分子自身の大きさと分子間力を全く無視する。そのような分子で構成される気体を理想上の気体という意味で理想気体ideal gasと呼ぶ。理想気体が振る舞う系を表現する基本関係式はエントロピー表示で以下のように与えられることが分かっている。
ただし、nは物質量で、Rは気体定数である。添え字の0はある任意の状態0での値を表す。単位の取り方によってRは異なった値を用いるので注意してほしい。例えば、圧力(atm)、体積(ℓ)、温度(K)、物質量(mol)の系であればR=0.082、圧力(psia)、体積(ft3)、温度(°R)、物質量(lb-mol)の系であればR=10.731となる。cは分子の内部運動の自由度で決まる正定数で、単原子分子よりなる理想気体では自由度が最も小さいので最小値3/2をとり、非理想気体では条件によってさらに大きくなる。さて、(37)式を体積Vについての偏微分をとると、
のような簡単な形になる。エントロピーSのVについての偏微分は(35)ですでに示されているので、偏微分の項を消去すると、以下の関係が導ける。
この式は高校化学で習う理想気体の状態方程式である。後の章で、この式が得られるまでの歴史を少し紹介するが、熱力学の基本関係式を知っていれば数学的に導くことができるものである。
さらに、(37)式を体積Uで偏微分を行うと、
なる式が得られる。上式の左辺は温度の定義式であり、その関係を用いるて偏微分の項を消去すると以下(39)式に帰結する。
この式は通常、
のように表記され、理想気体の内部エネルギーを表す式として知られている。これも有名な式で丸暗記の対象になったりもするのだが、基本関係式が分かれば簡単に導くことができる。これらの導出過程から分かるとおり、基本関係式は古典力学における運動方程式のようなものであり、基本関係式を知っていれば自分の使いやすいさまざまな形の関係式に展開することができる。なお、ここまでの議論はエントロピー表示の基本関係式をもとに進めてきたが、エネルギー表示の基本関係式から出発しても同じ結果が得られる。エネルギー表示の理想気体の基本関係式は(37)式をUについて解くことで得ることができ、次のような形で与えられる。
余力があればこの式から出発して理想気体の状態方程式を導出してみると面白いだろう。