界面張力を考えるときはゴム風船を考えると分かりやすい。今、半径rの試験管に入った水を考えると、図のようなメニスカスができると思うが、空気の層が風船のように膨らんでいるイメージをつくると界面張力σなるものを易しく理解することができる。
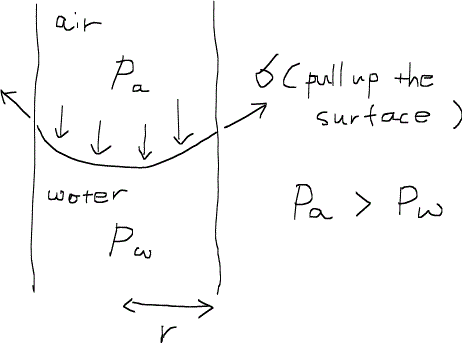
この場合、空気の圧力の方が水の圧力より高くなっている。また、壁が風船の膜を引っ張る力こそが界面張力である。界面に注目して力の釣り合いを見てみると、空気が膜を下方向に押す力に対して、水が膜に上に押し返す力+膜を壁が引っ張り上げる力(界面張力の鉛直方向成分)が拮抗している形になっている。風船の膜を三重点で押さえているとイメージすればよい。
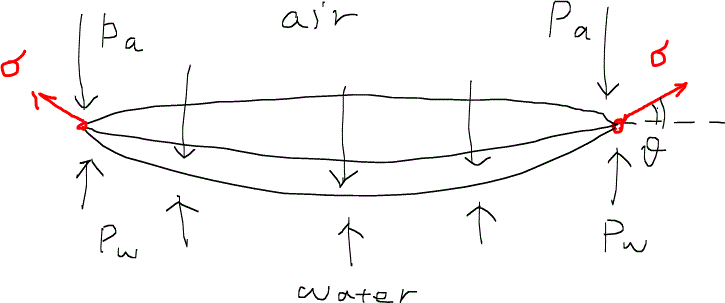
つまり、式にすると次のように関連付けることができる。
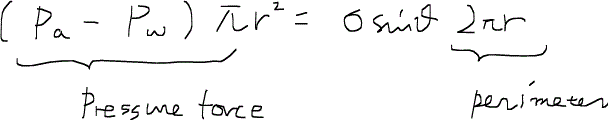
なお、界面のドームは次のように曲率半径Rの大きな球の一部と見なすことができる。
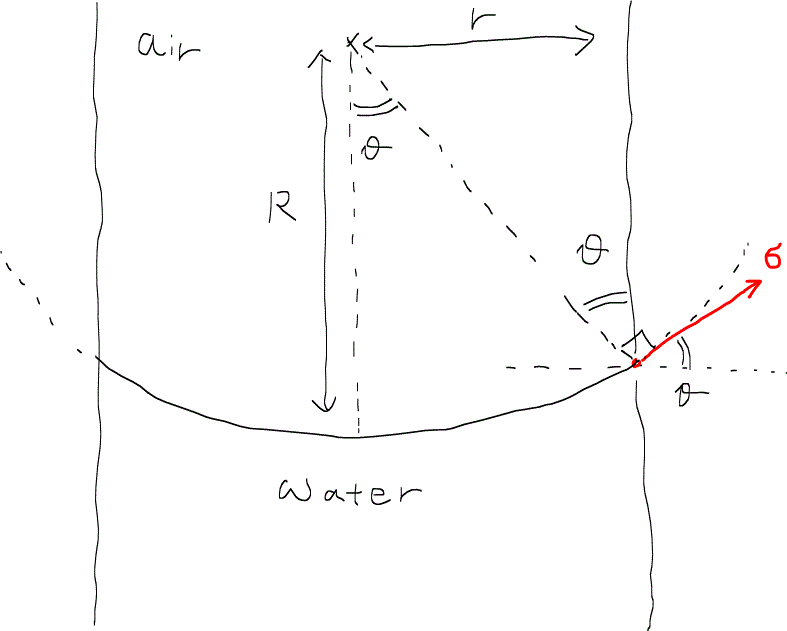
つまり、
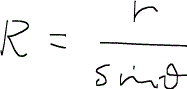
であるので、圧力差の式は曲率半径を用いればきれいに記述することができ、結局、
![]()
になることが分かる。界面張力は物質のペアによって固有の値を示すので、Rが小さくなれば巨大な圧力差が生じることがこの式から示唆されている。毛細管現象はこの圧力差によって引き起こされるという訳である。ちなみに、この式はラプラス方程式Laplace equationと呼ばれており、圧力差Δpのことを毛細管圧力capillary pressureと呼び、pcと表す。
![]()
非常に小さな孔隙に注目している貯留層工学では当然Rが小さくなるので、毛細管圧力の影響が無視できなくなる。この事実は技術者にとって大変大きな意味を持っており、貯留層工学の悩ましいところでもあり、面白いところでもある。








