さて、ここではフラッシュ計算を行なうにあたっての拘束条件を整理しておく。まず、温度、圧力、成分組成によって与えられた条件のもと、系が液体1相、気液2相、気体1相のいずれかの状態で平衡状態に達するものと仮定すると、物質収支的に次に示す式を常に満たさなければならない。
(61) 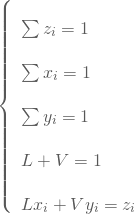
ただし、![]() は初期に与えられる成分
は初期に与えられる成分![]() のモル分率、
のモル分率、![]() は平衡状態の液相における成分
は平衡状態の液相における成分![]() のモル分率、
のモル分率、![]() は平衡状態の気相における成分
は平衡状態の気相における成分![]() のモル分率、
のモル分率、![]() は液相のモル分率、
は液相のモル分率、![]() は気相のモル分率を示している。なお、
は気相のモル分率を示している。なお、![]() はフィードであり既知であるから、ここでの目的は結局以上の式を満足するように
はフィードであり既知であるから、ここでの目的は結局以上の式を満足するように![]() 、
、![]() 、
、![]() 、
、![]() を決定することとなる。
を決定することとなる。
また、フラッシュ計算の過程で気液平衡定数(K値)を求めるのでその定義も以下に示しておく。
(62) ![]()
平衡定数を用いると、![]() と
と![]() は次のように表現することができる。
は次のように表現することができる。
(63) ![]()
(64) ![]()
当然のことながら平衡定数は温度、圧力、組成によって変化する訳で、これが求まらなければ![]() と
と![]() は導くことができない。したがって、フラッシュ計算とは実質的に平衡定数を求める演算と言ってよいだろう。
は導くことができない。したがって、フラッシュ計算とは実質的に平衡定数を求める演算と言ってよいだろう。








