ギブズ・デュエムの式

ここまで示強性変数を基本関係式の自然な変数にとる表記について述べてきた。ここでは、示強性変数を使うことは示量性変数を使うことと何が異なるのか、ということを考えよう。示量性変数である $S$ , $V$ , $N$ はエネルギー表示の基本関係式において自然な変数であると同時にそれぞれが独立して振舞うことができる。つまり、 $S$ , $V$ , $N$ を適当に与えれば、それに対応する平衡状態が実現されるわけである。では、示強性変数も自由に与えることができるのだろうか？　示強性変数のうち、 $T$ と $p$ は簡単に計測可能であり、実験などでもコントロールもしやすいので便利な変数ではあるのだが、実は平衡状態において $T$ , $p$ , $\mu$ といった示強性変数は完全に独立して変化させることはできない。そのような示強性変数の動き方に関する制限を規定するのが以下に示すギブズ・デュエムの式Gibbs-Duhem equationである。

(87) $\begin{equation*} \begin{split} Nd\mu = -SdT+Vdp \end{split} \end{equation*}$

せっかくなのでギブズ・デュエムの式を導出してみよう。

まず、ギブズエネルギーは物質量 $n$ について、次のような性質を持っている。ただし、 $N_A$ はアボガドロ数である。

(88) $\begin{equation*} \begin{split} G(T, p, nN_A)=nG(T, p, N_A) \end{split} \end{equation*}$

誤解を恐れずに言えば、これは $G$ と $N$ が示量性変数であり、 $T$ と $p$ が示強性変数だからである。すなわち、 $T$ と $p$ を固定したまま粒子数を $n$ 倍にすると、ギブズエネルギーも $n$ 倍になることを示している。数学的にはギブズエネルギーが、示量性変数である $N$ についての（一次）同次関数なので成り立つ式であると言える。なお、一次同次関数とは正の実定数 $\alpha$ を与えたときに次のような関係を満たす関数のことである。同次性のより正確な議論については別途詳しく掲載することにするので参考にしてほしい。

(89) $\begin{equation*} \begin{split} f(\alpha{x_1}, \alpha{x_2}, \cdots, \alpha{x_p})=\alpha{f}(x_1, x_2, \cdots, x_p) \end{split} \end{equation*}$

ところで、粒子数の定義より $N=nN_A$ なので、(88)式は次のようにも書ける。

(90) $\begin{equation*} \begin{split} G(T, p, N)=nG(T, p, N_A) \end{split} \end{equation*}$

この式を $n$ で偏微分すると次ののような式が得られる。

(91) $\begin{equation*} \begin{split} \frac{\partial{G(T, p, N)}}{\partial{n}}=G(T, p, N_A) \end{split} \end{equation*}$

ここで、表4の化学ポテンシャルの定義式である、

(92) $\begin{equation*} \begin{split} \mu=\frac{\partial{G(T, p, N)}}{\partial{N}} \end{split} \end{equation*}$

なる式に少し変数変換を施すと、

(93) $\begin{equation*} \begin{split} \mu&=\frac{\partial{G(T, p, N)}}{\partial{N}}\\ &=\frac{\partial{G(T, p, N)}}{\partial{n}}\frac{\partial{n}}{\partial{N}}\\ &=\frac{\partial{G(T, p, N)}}{\partial{n}}\frac{1}{N_A} \end{split} \end{equation*}$

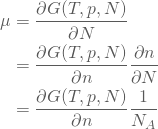
のようになるので、(91)式の左辺を消去すると、次の式が得られる。

(94) $\begin{equation*} \begin{split} N_A\mu=G(T, p, N_A) \end{split} \end{equation*}$

ただし、

(95) $\begin{equation*} \begin{split} G(T, p, N_A) = N_A{G}(T, p, 1) \end{split} \end{equation*}$

であるので、結局、次の斬新な式を得ることができる。

(96) $\begin{equation*} \begin{split} \mu=G(T, p, 1) \end{split} \end{equation*}$

この式から明らかなように化学ポテンシャル $\mu$ は $T$ と $p$ のみの関数であるので、この式はより明示的に次のように書ける。

(97) $\begin{equation*} \begin{split} \mu{(T, p)}=G(T, p, 1) \end{split} \end{equation*}$

この式は非常に意義深い。化学ポテンシャルの定義は本来表4で与えられているとおり、内部エネルギー、ヘルムホルツエネルギー、エンタルピー、ギブズエネルギーのいずれかを粒子数で偏微分したものである。しかし、実質的には(97)式で与えられているように、粒子1個あたりのギブズエネルギーが化学ポテンシャルにほかならないことが分かる。教科書によっては1モルあたりのギブズエネルギーと書いてある場合もあるが、そのあたりは変数変換で自由にできるので物理的な意味は同じである。いずれにせよ、もともと粒子1個あたり（または1モルあたり）のギブズエネルギーという量に物理的な意味があったのではなく、ギブズエネルギーが一次同次性を満足するという仮定のもと数学的な展開の末に導出された解釈だと言える。

議論をさらに進めよう。アボガドロ数 $N_A$ の代わりに粒子数 $N$ を用いて、(94)式を書き直すと次のようになる。

(98) $\begin{equation*} \begin{split} G(T, p, N) = \mu{N} \end{split} \end{equation*}$