多孔質媒体が円柱状のチューブcylindrical tubeの集合によってできていると仮定しよう。
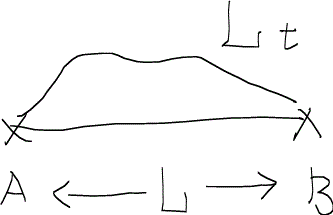
このときに、ハーゲン・ポワズイユ方程式Hagen-Poiseuille equationを使うと1本のチューブを流れるニュートン流体の流量は次のように書くことができる。ただし、Rはチューブの半径、Ltはチューブの長さである。チューブは曲がっていてもかまわない。
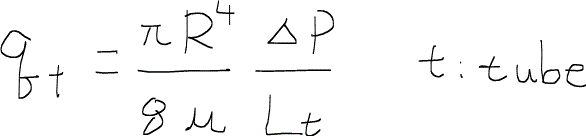
流体の流れが定常層流steady laminar flowだと仮定すると、平均流速は次のように書くことができる。
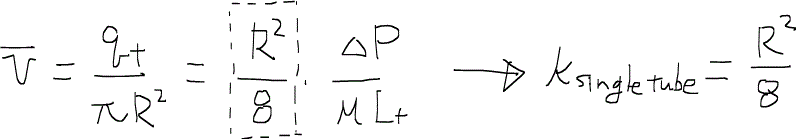
ただし、ここでの流速は
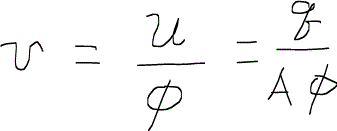
と与えられ、間隙速度interstitial velocityと呼ばれる。実際に空隙の中を流体が流れる速度である。また、uはダルシー流速と呼ばれるもので孔隙率が100%だと仮定した時の速度であり見かけ上の速度superficial velocityとも言われる。いずれも単位は[L/T]である。ダルシー流速は、
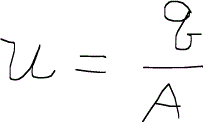
と定義される。
さてここで、チューブ単体ではなくREVで代表されるある塊として孔隙を見てみよう。ここに流体を流してみると、チューブとしてモデル化されたものも、REVでモデル化されたものも、同じ時間をかけて流体が通り抜けなくてはならない。つまり、
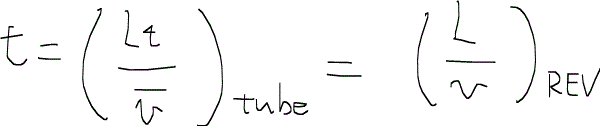
となる。チューブで代表されたモデルは先のハーゲンポワズイユの式を、REVで代表されたモデルはダルシーの式が使えることを考えると、上の式は次のように展開することができる。
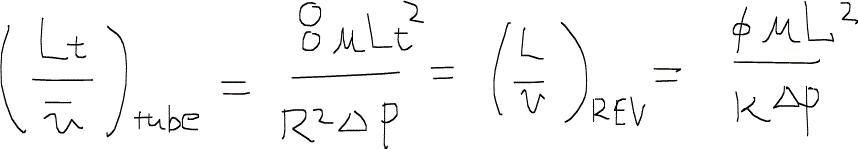
浸透率kについて上の式を解くと、結局次のようになる。
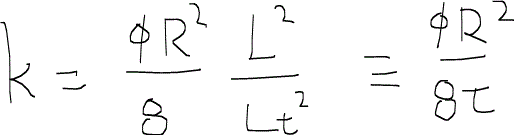
ここで新しい係数τを定義しているが、屈曲度tortuosityと呼ばれる量である。
![]()
定性的にはチューブがどのくらい曲がりくねっているかを示す値として知られる。
このように、浸透率はチューブの半径、孔隙率、屈曲度に依存することが分かる。とくにチューブ半径の与える影響が特に大きい。








