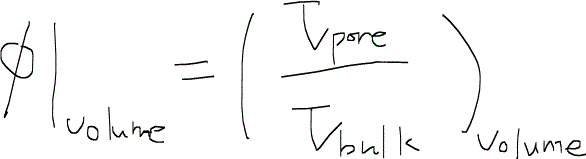孔隙率は、多孔質媒体の物性のうち、もっとも直感的なもののひとつであろう。
直感的に理解できる孔隙率という物性だが、少し面白い概念を導入してもう少し深く考えてみる。というのも、孔隙体積なるものを平均的に求める必要があるからである。いま、ミクロな視点に立って、多孔質媒体を考えると、究極的には次のようなモデルを考えることができる。
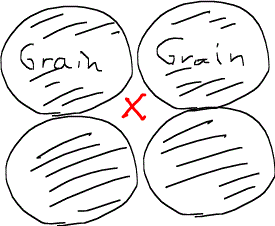
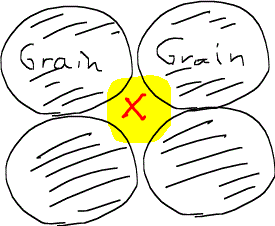
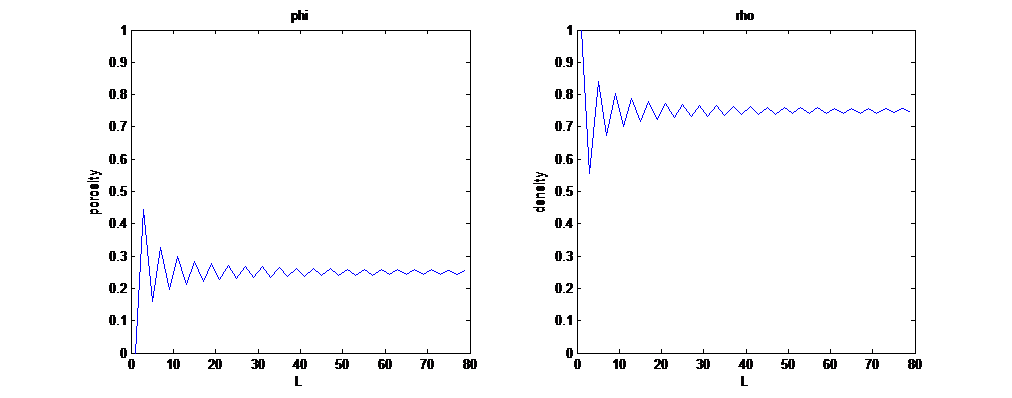
ここで、視点の中心を赤い×印の点に置いて考えると、この場所の孔隙率は100%である。視点の中心はそのままで、少し考える範囲を黄色い部分まで広げてみると、岩石が入ってくるので、孔隙率は例えば70%などになる。
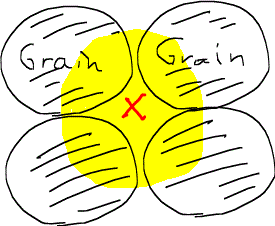
さらにその半径を広げていくと、
のようになり、孔隙率は局所的に極小値になる。ここからまた半径を広げていくと孔隙率は上昇に転じるが元の100%まで戻ることはなく、以後半径の増加に伴って振動を繰り返す。もし半径が十分大きくなれば、孔隙率は一定の値に収束する。収束したときに、黄色い部分が示す体積のことをREV(代表要素体積representative elementary volume)と呼ぶ。振動の様子を漫画的にグラフ化すると次のようになる。この例の場合、孔隙率は25%に収束する。
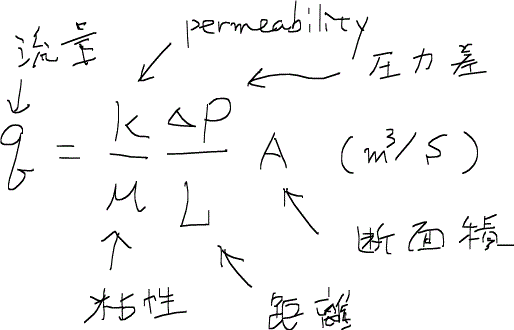
REVの大小は統計的な不均質性を表しており、体積と直接的な関係がある孔隙率をどのように求めたらよいかを示唆している。多孔質媒体の物性を代表する値でもう一つの主役は浸透率であるが、単純な平均では求められない。なぜなら、浸透率がダルシーの法則という経験式から導かれる値であり、種々の仮定やモデル化が内包されているのでさらに深い考察(カルマン・コゼニー方程式)が必要になる。ちなみに、ダルシーの式は次のように与えられている。