宇宙で普遍的に成り立つと思われている法則のひとつにエネルギー保存の法則law of conservation of energyがある。エネルギー保存の法則が物理学で占める地位は金科玉条級であり、古典力学、電磁気学、熱力学、統計力学、相対論、量子論などすべての基礎的な物理学でエネルギー保存の法則が成り立つ。現代物理学が勃興してからは幾度となく疑いの目が向けられてきたもののその堅牢さはいまだ揺るがず、現在の物理学の枠組みでは最も普遍的と言ってよい原理である。
ただし、この法則で保存されるエネルギーとは全エネルギーである。そして全エネルギーEは一般に以下のように記述することができる。
エネルギーの出入りがない系ではこの全エネルギーが厳密に保存されることになっている。全エネルギーは、系全体としての運動エネルギーE全体運動と系全体としての位置エネルギーE全体位置、そしてそれ以外のエネルギーE内部の和として表現される。系全体の運動エネルギーは並進だけでなく回転によるものも含まれている。高校物理で学習する古典力学では、運動エネルギーこと並進エネルギーと位置エネルギーだけでエネルギー保存の式を作ったと思う。図1は摩擦のない滑らかな斜面を球が高い場所から低い場所に滑り落ちる様子を模式的に示したものである。

図1 古典力学での質点の運動
このモデルでのエネルギー保存の式は以下のように表現してきたと思う。
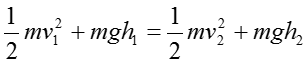 (4)
(4)
右辺左辺ともに第一項が運動エネルギー、第二項が位置エネルギーである。単純な式だが球が滑り落ちていったときの任意の場所での速度を解析的に求めることができ、例えば初速度が0であれば、
![]() (5)
(5)
と求まる。しかしこの式は回転エネルギーと内部エネルギーが含まれていない。これは高校で勉強するニュートンの古典力学では物体が大きさを持たず変形を伴わない「質点point mass」として定義されているためである。質点であれば、大きさという概念を持たないため回転エネルギーの変化は考慮する必要がなく、さらに摩擦を無視しているので振動、熱、音などへのエネルギー変化も存在しない。
しかし、実際の現象では運動エネルギーと位置エネルギーが上に挙げたような異なった種類のエネルギーへ変化することを考慮する必要がある。もしも物体が質点と仮定できない現実的な現象を厳密に表現するならば、図2に示すようにエネルギーも物質も通さない壁で系全体を囲った上で、エネルギー保存の式を次のように書きなおす必要がある。
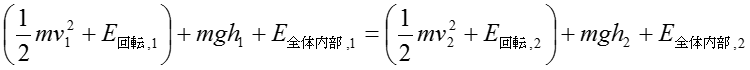 (6)
(6)
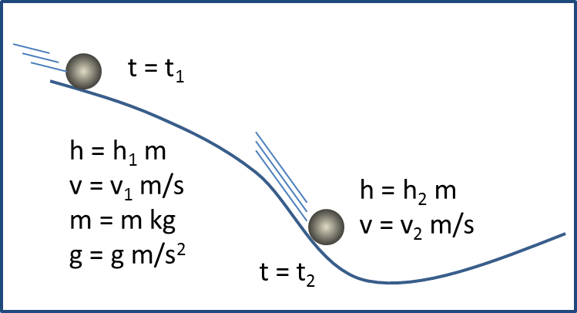
図2 古典力学での閉鎖系における質点の運動
このように現実世界でのふるまいを厳密に表現するには原則的に系が持つすべてのエネルギーをもれなく合算してエネルギー保存を議論する必要がある。ただし、現実的なマクロな系を考える場合でも、惑星の運動を考える場合などは、系に比べて惑星が十分小さく質点と見なせるので(4)式が十分な精度で成り立つ。一方で、我々が熱力学で扱おうとしている、ひとつの場所に静かに固定された系の中での気体の振る舞いといった現象の観察であれば、「系全体としての」運動エネルギーと位置エネルギーの変化は無視できる。つまり熱力学において、孤立した系で保存されるべきエネルギーは内部エネルギーのみと見なすことができ、特別な記号Uを与える。
![]() (7)
(7)
なお、非常に密度の大きいガスや液体が、系の上方に偏っている初期条件を想定すると、流体が重力によって移動し位置エネルギー変化が生じるので、エネルギー保存を表す(3)式は以下のようになる。
![]() (8)
(8)
本書で議論する熱力学では(7)式が成り立つことを前提とするが、もしその前提条件が成り立たない場合でも必要に応じて(8)式のように系の全エネルギーを表現する式を書き直せばよい。








