臨界点付近での相挙動の評価など数値的に平衡状態を決定することが難しい場合には、フュガシティの一致を利用したSSIニュートン法ではなく、より高次の最適化手法を利用しなければならない状況が稀に生じる。そのような場合はフュガシティが一致する点を探す求根問題ではなく、ギブズエネルギーが最小になる点を探す最小化に置き換えて、二次の最適化アルゴリズムを利用する。
独立変数を液相のモル分率![]() と仮定すると、ギブズエネルギー、ギブズエネルギーの勾配ベクトルgradient vector、ヘッセ行列Hessian matrixは次のように与えられる。
と仮定すると、ギブズエネルギー、ギブズエネルギーの勾配ベクトルgradient vector、ヘッセ行列Hessian matrixは次のように与えられる。
(106) 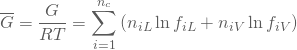
(107) 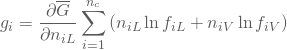
(108) ![]()
ただし、勾配ベクトルとヘッセ行列については各成分のみを抜き出してある。なお、気相のモル分率![]() を独立変数であると仮定した場合のヘッセ行列は次のようになる。
を独立変数であると仮定した場合のヘッセ行列は次のようになる。
(109) ![]()
さて、ギブズエネルギーの最小化問題を解くにはまず次のような線形方程式を解いてニュートン方向Newton directionなるものを決める必要がある。
(110) ![]()
ここでの![]() がニュートン方向であり更新ベクトルに相当する。ニュートン方向が求まればギブズエネルギーの最小値は次の漸化式によって逐次的に求めることができる。
がニュートン方向であり更新ベクトルに相当する。ニュートン方向が求まればギブズエネルギーの最小値は次の漸化式によって逐次的に求めることができる。
(111) ![]()
収束の判定は例えば次のような条件を確認すればよい。
(112) ![]()
ただし、![]() は許容誤差である。
は許容誤差である。








