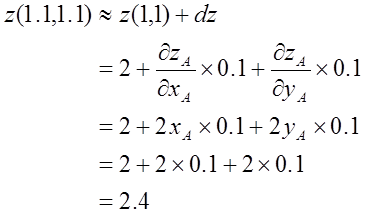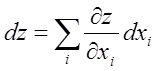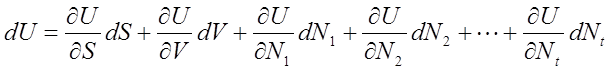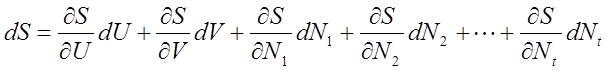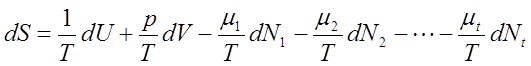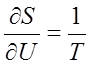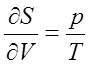熱力学ではすでに何度も述べているとおり、平衡状態と、ある平衡状態から別の平衡状態に移る遷移のみを記述することを目的としたアプローチである。今までの議論では、エントロピーやエネルギーを、状態量を使って記述することで平衡状態を記述することを目的としていた。
そこで次はついに、平衡状態間の遷移を記述することを試みる。非平衡状態ではエントロピーが定義できないので、熱力学を用いて系を記述することはできないが、ある平衡状態から状態量を少しだけずらしたときに、系がどのように移り変わるかということは偏微分を使って表すことができる。
数学が得意な読者は読み飛ばしてほしいのだが、偏微分とは多変数関数を微分するときに必要となる方法である。意外とこのあたりがよく分かっていないと議論が進まないのでくどいながらも少し解説しておく。
まず、多変数関数とは入力feedする変数が複数個ある関数を言う。例えば
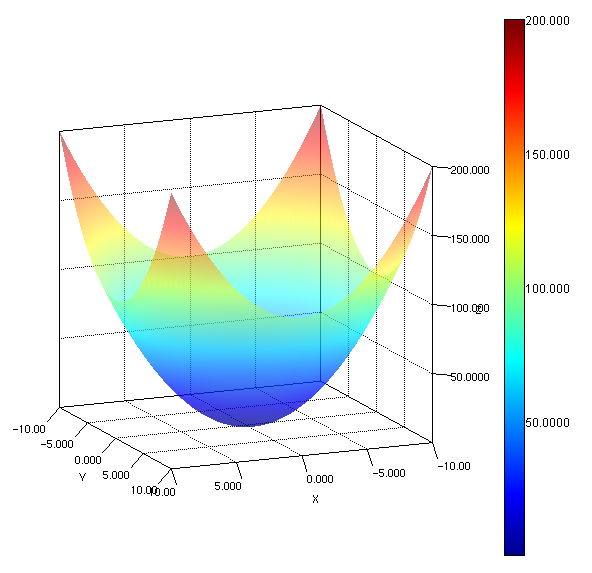
は二変数関数であり、もっとも簡単な多変数関数のひとつである。変数と言うのはxとyのことで、それぞれが独立に動くことができる。すなわちxとyをさまざまに動かして関数zの値を計算し、x–y–z空間にその値をプロットすると以下のようになる。縦軸が関数zの値である。注意してほしいのはxとyは独立に動くことのできる変数であり、zはそれらにしたがって決まる値である。
図3 二変数関数のとる値の例
さて今、点A(x, y) = (1, 1)からほんの少しだけ離れた点B(x, y) = (1.1, 1.1)での関数の値を、点Aでの関数の情報のみを用いて求めるためにはどうしたらよいだろうか。今はx, yの定義域すべてで関数が分かっているので単純に関数zに(x, y) = (1.1, 1.1)を代入すればその値が直接求まるのだが、点Aのみでしか関数zの形が分からない場合の話だと思って聞いてほしい。アイデアとしては、x方向、y方向それぞれにどれだけzの増分があるかを計算し、足し合わせればよい訳である。偏微分自体についての説明は割愛するが、関数zがx, yそれぞれについて偏微分可能であれば、以下のような演算となる。ただしdzは点Aから少しだけ場所を移動したことによる関数zの増分を表す。
簡単な例だが点Aでの情報だけで、点Bでの関数zの値z(1.1, 1.1)を近似することができた。今回はほんの少しと言っても0.1動かしたので、実際にz(1.1, 1.1)を計算した値である2.42(= 1.12+1.12)から多少逸脱していることが分かる。この逸脱の幅は微分による近似の仕方に依存するものであり、今回は一次微分のみで近似したために顕在化したものである。一次微分で近似する際の近似の精度を一次の精度と言う。より正確な近似をするためには高次high-orderの微分を用いる必要があるが、きわめて微小な量を動かすことが分かっている場合は一次の近似でも十分である。動かす幅を小さくすればするほど真の値と偏微分で求めた値の差は限りなく小さくなっていくからだ。
このように、ある点から微小な変位を与えた場合に多変数関数がどれだけ変化があるかを示す計算を全微分total derivativeという。全微分は多変数関数ならではの計算であるが、実質的には微分そのものなので、多変数関数であることが分かっている場合は単に微分とも呼ぶ。二変数関数のケースを例にとって全微分を一般化すると、以下のように書くことができる。
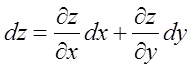 (28)
(28)
また、(28)式は容易により一般的な表現に拡張でき次のように書ける。
この知識を使って、ある平衡状態から少しだけ離れた別の平衡状態を計算してみよう。まず、ある平衡状態が存在したときに、その特徴は基本関係式で完全に表すことができることはすでに述べた。エントロピー表示の基本関係式であれば(9)式、エネルギー表示の基本関係式であれば(10)式である。
![]() (10)
(10)
エネルギー表示の基本関係式である(10)式を用いると、平衡状態にある系の状態変数を少しだけ動かしたときのエネルギーの増分は、以下のような全微分で求めることができる。
ここで、示強性変数の定義式である(22)、(24)、(25)の各式を用いると、(30)式は次のように書きなおすことができる。
このように、全微分を用いると、状態変数の値がわずかに異なる2つの平衡状態におけるエネルギー差を近似的に表すことができることがわかる。
エントロピー表示の基本関係式とエネルギー表示の基本関係式は完全に等価であり、どちらかが成り立てばもう片方も同じように成り立つ。そこで、エントロピー表示の基本方程式の全微分も求めておく。
先に求めた(31)式は非常に有名な式であり、それに比べると(32)式はあまりなじみがないと思う。ところで、(9)式と(10)式は等価であるとすでに述べた。すると、(31)式と(32)式は変数によらず常に同時に成り立たなければならない。この要請を満たすためには、多項式の係数の比較をすればよい。比較しやすくするために、(31)式の両辺をT(>0)で割って以下のように整えてみる。
(32)式と(33)式が変数によらず同時に成り立つ必要があるので、その係数を比較すると、
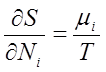 (36)
(36)
のように関係が導ける。(34)式は温度の定義式として登場した(22)式そのものである。残りの(35)式や(36)式も示量性変数と示強性変数を結び付ける普遍的な式と言える。これらの関係は基本関係式から理想気体の状態方程式を導くのに使える。