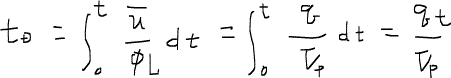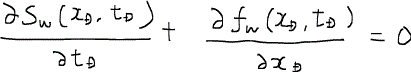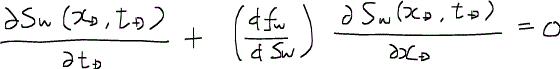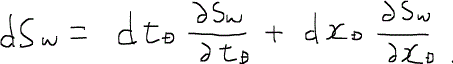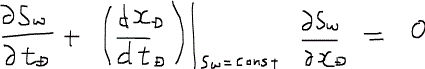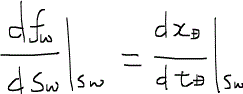バックレイ・レバレット理論

ここではバックレイBuckleyおよびレバレットLeverettにより提唱された理論（Buckley-Leverett theory, 1942年）に従って、質量保存の式を解いて飽和率分布を求めてみる。まず、時間と空間を一般化するために、それぞれ無次元量に変数変換する。

（53）

（54）

ここでの無次元時間t_Dは、PVI（pore volume injected）と呼ばれている量であり、つまり孔隙体積の何倍の流体が圧入されたかを示している。例えばt_D = 1であれば、孔隙体積と同じ量の流体が圧入された時点を示しており、理想的な置換ではすべての油が排出される瞬間ということになる。V_pは孔隙体積である。さて、この無次元量を用いて質量保存の式を記述すると、すでに議論した通り次の式に帰着する。

（55）

ここで、連鎖律chain ruleを適用すると、次のように書き換えられる。

（56）

この式は、時間と空間に関する一次の二変数偏微分方程式である。ここからは初期条件と境界条件を考慮してこの式を解いていくことにする。

まず、水の飽和率の全微分を求めることから始める。水の飽和率は時間と距離の関数であるので、

（57）

なる式が得られる。この式を変形すると、

（58）

（58）式と（56）式を見比べると、

（59）

なる大変興味深い式が得られる。この式が意味するところは、ある飽和率におけるフラクショナルフロー曲線の傾きは、その飽和率の速度に等しいということである。

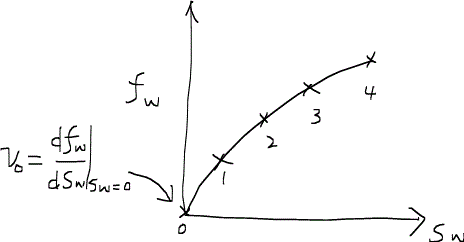
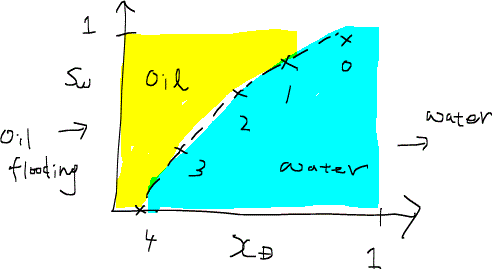
あとは初期条件を与えれば、任意の場所、時間での飽和率分布を求めることができる。例えば、次のような形状を持つフラクショナルフロー曲線について、二つのケースを試してみよう。

• 油相に水を圧入（S_WI = 0, S_WJ = 1）

ここでの下付き字のIは初期条件Initial condition、Jは圧入条件inJection conditionを表す。与えられたフラクショナルフロー曲線は、S_w = 0のときの速度が最も早くなることを示唆している。時間がたつと、最も速度の速いS_W = 0の部分と最も遅いS_W = 1の部分の差は広がっていく。

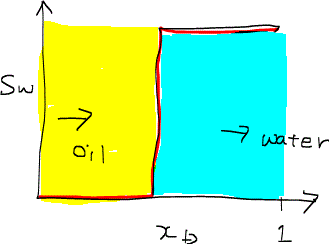
• 水相に油を圧入（SWI = 1, SWJ = 0）

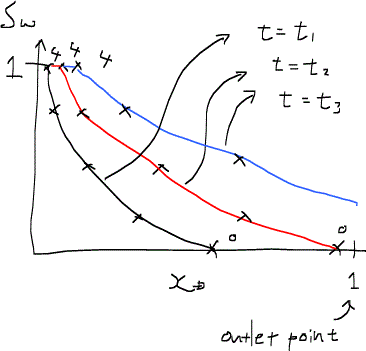
逆に、水相に油を圧入すると、単純にフラクショナルフロー曲線を解釈すると次のような飽和率分布が得られるはずである。

しかし、この結果は物理現象に反している実際には生じえない。なぜなら、置換フロントの飽和率はSW = 1（全部水）であり、その速度はポイント4のもので常に最も遅い。しかし、後から来たはずのSW < 1 の部分がポイント4追い抜いてしまっている。実際はどのような置換フロントが形成されるかというと、次のように図示できる。これは、いわゆるピストン状の置換piston-like displacementで、効率のよい置換プロセスである。

このように、速く走りたい物体が、より先頭にいる遅い物体を追い越せないときは、物理的にショックが生じる。1車線の道で遅い車がたらたら走っていると渋滞が生じるのと同じ原理である。ショックにより生じた不連続な置換フロントのことをショックフロントshock frontなどと言う。ショックフロントの位置は単純な微分の計算では求められないので、続く記事では物理的な制約を組み込んでその位置を求めていくことにする。