now♯

half tone higher than now

ニュートン・ラフソン法

SSI法はK値の初期推定値の精度が悪くても速やかに収束解を得ることができる手法である。しかし逆に解に近づくにつれて収束速度が低下するという特性を持っている。したがって通常SSI法は近似解を得る際の効率性と正確性を向上させる目的でニュートン・ラフソン法と組み合わせて用いられることが多い。ニュートン・ラフソン法は汎用的な求根アルゴリズムの一つであり二次の収束速度quadratic convergence rateを持つ。初期予測解の精度が高い場合は速やかに収束して精度の高い近似解を与えるため、SSI法によって求められた近似解を初期値としてニュートン・ラフソン法を実行することで非常に高速かつ正確な求解が可能となる。

そこでSSI法のプラスアルファ的な項目として、フラッシュ計算においてニュートン・ラフソン法をどのように適用すべきかという問題を紹介しておく。なおラッシュフォード・ライス方程式を解いた際のニュートン・ラフソン法とは求めるパラメータが異なるので注意してほしい。ここでは二相のPTフラッシュ計算を前提とする。まず、相平衡の条件はフュガシティの一致によって次のように表現できるのであった。

(92)   \begin{equation*} f_{iL}(\vec{N}_L)=f_{iV}(\vec{N}_V)\quad \forall{i} \end{equation*}

ただし、ここではモル分率の代わりに実際のモル数Nを計算に用いており次のように定義されている。

(93)   \begin{equation*} N_{iL}=x_i N_L \end{equation*}

(94)   \begin{equation*} N_{iV}=y_i N_V \end{equation*}

(95)   \begin{equation*} N_i=z_i N \end{equation*}

なお、N_{iL}とN_{iV}の間には次の関係が成り立っており、N_iはフィードのモル数であり既知の量である。

(96)   \begin{equation*} N_{iL}=N_i -N_{iV} \end{equation*}

また、ベクトル\vec{N}は各相に含まれる成分ごとのモル数を格納するベクトルである。

(97)   \begin{equation*} \vec{N}_L=\left( N_{1L}\quad N_{2L}\quad \cdots \quad N_{n_c L} \right)^T \end{equation*}

(98)   \begin{equation*} \vec{N}_V=\left( N_{1V}\quad N_{2V}\quad \cdots \quad N_{n_c V} \right)^T \end{equation*}

このとき、次のような関数F_iを定義すると、この関数の根を求めることと（92）式を解くことが数学的に同等になることが分かる。なお関数F_iは残差関数residual functionと呼ばれる。

(99)   \begin{equation*} F_{i}=f_{iV}(\vec{N}_V) -f_{iL}(\vec{N}_L) \quad \forall{i} \end{equation*}

したがって、平衡状態の導出するには、n_c元非線形連立方程式である次の式をN_{iL}またはN_{iV}について解くことに他ならないことが分かる。

(100)   \begin{equation*} \vec{F}=\vec{0} \end{equation*}

ただし、\vec{F}は各方程式を格納したn_c次元の縦ベクトルである。

(101)   \begin{equation*} \vec{F}=\left( F_1 \quad F_2 \quad \cdots F_n_c \right)^T \end{equation*}

この方程式は非線形連立方程式であり、数値的に近似解を求めることになるのだが、そこで用いられるのがニュートン・ラフソン法である。気相のモル数について方程式を解くことを前提にすると、近似解の漸化式（ニュートン・アップデートNewton updateとも呼ばれる）は次のように書くことができる。

(102)   \begin{equation*} \vec{N}_V^{n+1} = \vec{N}_V^n -J^{-1} \vec{F}^n \end{equation*}

なお、ここでのJ^{-1}はヤコビ行列Jacobian matrixの逆行列であり、ヤコビ行列Jの各要素は次のように与えられる。

(103)   \begin{equation*} J=\left[ \begin{matrix} \frac{\partial{F_1}}{\partial{N_{1V}}} & \cdots & \frac{\partial{F_1}}{\partial{N_{n_cV}}} \\ \vdots & \ddots & \vdots\\ \frac{\partial{F_n_c}}{\partial{N_{1V}}} & \cdots & \frac{\partial{F_n_c}}{\partial{N_{n_cV}}} \end{matrix} \right] \end{equation*}

ただし、

(104)   \begin{equation*} \frac{\partial{F_i}}{\partial{N_{jV}}} = \frac{\partial{f_{iV}}}{\partial{N_{jV}}} - \frac{\partial{f_{iL}}}{\partial{N_{jV}}} = \frac{\partial{f_{iV}}}{\partial{N_{jV}}} + \frac{\partial{f_{iL}}}{\partial{N_{jL}}} \end{equation*}

これらの要素を具体的に展開すると次のような表現が得られる。

(105)   \begin{equation*} \frac{\partial{F_i}}{\partial{N_{jV}}} = \frac{1}{N_V} \sum_{k=1}^{n_c -1} \frac{\partial{f_{iV}}}{\partial{y_{k}}}(\delta_{k,j}-y_k) + \frac{1}{N-N_V} \sum_{k=1}^{n_c -1} \frac{\partial{f_{iL}}}{\partial{x_{k}}}(\delta_{k,j}-x_k) \end{equation*}

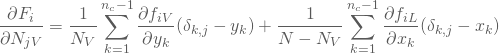
ニュートン・アップデートの式を見て分かるとおり、この手法では一次の導関数のみしか用いられていないため、より複雑な相挙動を解く際に収束性の問題が生じる場合がある。そのような時は平衡状態においてギブズエネルギーが最小になることを利用して二次の最適化問題として取り扱う。