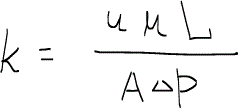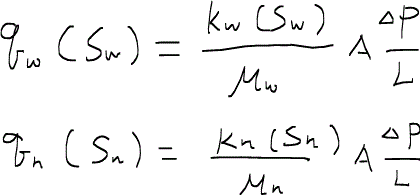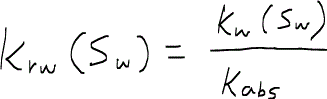相対浸透率とは

ところで、浸透率はどのように求めるのだったろうか。浸透率は多孔質媒体中の流れを表現するダルシーの式によって定義される量であったので、ダルシーの式自体が浸透率kの導出式と言える。

ただし、uは流速、μは粘性、Lは媒体の長さ、Aは媒体の断面積、Δpは流体の入口と出口の間にかかる圧力差である。

しかしこの導出方法は一相流のときのものである。貯留層内の流体流動を観察すると、例えばガス油や油水のような二相流になる。このようなときに浸透率はどのように定義されるべきなのかだろうか。

二相流をコアの中に流す場合、一相流のときと異なりそれぞれの相が安定して流れるようになるまで少し時間がかかる。それぞれの相の流速が変化しなくなったときの状態を定常状態steady stateと言う。実際にこの実験を行うと時間がかかるので非常に高価である。

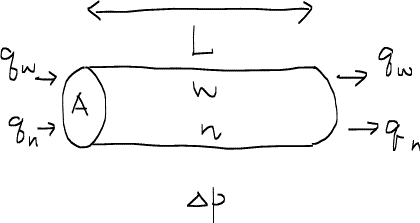
さて、定常状態の二相流について、ダルシーの法則を用いてそれぞれの相を別々に表現すると次のようになる。ただし、下付き字のwはコアに対して濡れ相を、nは非濡れ相を表している。

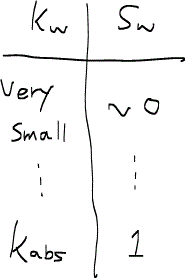
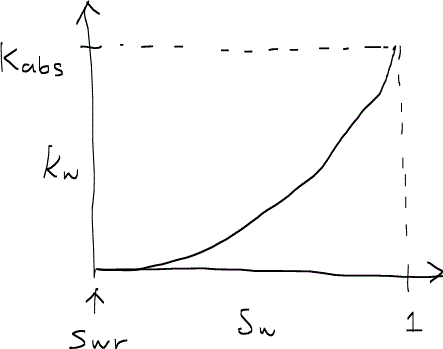
つまり、流量qと浸透率kがそれぞれ飽和率Sに依存する訳である。流量qが飽和率Sに依存するというのは直観的に理解できよう。二相流の浸透率が飽和率に依存するということについて説明しよう。例えば濡れ相についてk_wとS_wをプロットしてみる。まずS_wが1（つまり濡れ相の一相流）のときは、濡れ相の浸透率k_wはもとの浸透率（絶対浸透率k_absと呼ぶ）と同じである。逆にS_wが0（すなわち非濡れ相の一相流）のとき濡れ相の流量は当然0になるからk_wも0となる。飽和率は0 < S_w < 1の領域を変化するが、飽和率が増えるにしたがって流れる濡れ相の流量も増えるので連続的にk_wも増えてゆく。