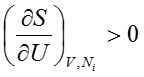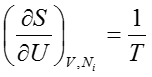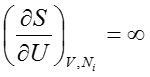仮定3は基本関係式の微分についての性質についての仮定であり、内部エネルギーの増加に伴い、系のエントロピーも増加すると主張している。すなわち、数式で表現すると以下のようになる。
なお、詳しくは後述するが上式の左辺は温度の定義式の逆数である。つまり、
である。驚くべきことに、「熱」力学であるにも拘らず、温度というものにほぼ触れずに議論を進めてきたわけであるが、こんなところで唐突に登場する。温度は実用的ではあるが、すでに述べたとおり示強性の変数であり熱力学の式変形に入り込むとややこしいので、あえて最後の最後まで論理展開には使わないスタンスで行く。とは言うものの、少し温度とエントロピーの関係を見てみよう。(13)式と(14)式より、以下の関係が示唆される。
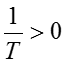 (15)
(15)
つまり仮定3を前提としている熱力学は、負の絶対温度を認めていない。非平衡状態に物理学の理論を拡張すると負の温度というものが登場することがあるのだが、何度も述べたように熱力学は平衡状態だけに注目して議論している。したがって、非平衡状態で何が起ころうと熱力学が不完全であることの反証にはならない。なお、Tが0になる点を絶対零度と呼ぶが、(16)式によるとT = 0はありえないので、実際にはT → +0の極限のことである。
温度に関する議論をもう少し進めると、温度が絶対零度になる点では、(14)式より、
となるので、すぐに以下のことが分かる。
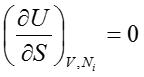 (18)
(18)
仮定3によると、
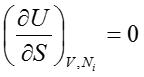
のときにエントロピーの下限値である0をとるとあるので、絶対零度においてエントロピーが0になることが分かる。このことは熱力学の第三法則third law of thermodynamicsとして知られているが、仮定3を公理とするスタンスでは熱力学の第三法則は仮定3のことを言い換えているに過ぎない。この法則は些細ではあるが、エントロピーという実態がつかみにくい量にも基準となる点が存在することを示している。