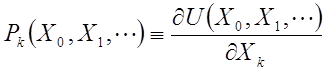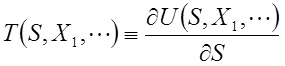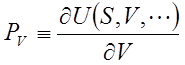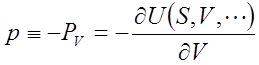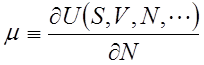仮定1を表現するために提示した（10）式をより一般化すると、次の（19）式のように書ける。
（10）
（19）
ここでのXは言うまでもなくエネルギーの自然な変数を一般化したものである。仮定3の良好な解析性により、エネルギーは常にその自然な変数の偏微分を得ることができる。
（20）
エネルギーの自然な変数Xは平衡状態で一意的に決まる量なので、それらの関数であるPもある平衡状態で一意的に決まるマクロ変数である。これをXkに共役conjugateな（エネルギー表示の）示強性変数と言い、以下のように表すことができる。
（21）
共役な変数のペアはさほど多くないと前述したが、より正確に言えば、共役な組み合わせになるのは、エネルギーの自然な変数であるS, V, Nのそれぞれについての3ペアということになる。そこでエネルギー表示の示強性変数を、S, V, Nについて求めてみると、おなじみの物理量が次々と出てくる。まず、エントロピーSに共役な示強性変数は記号Tと温度temperatureという名前を特別に与える。
（22）
次に、体積Vに共役な示強性変数は記号PVで表される。ここからさらにPVの符号を反転させたものが圧力pressureであり、pという記号を与える。参考書によっては圧力を大文字Pで与えることもあるが、貯留層シミュレータの世界では小文字で表記するのが一般的なようである。
（23）
（24）
最後に粒子数Nに共役な示強性変数PNは、特別な記号μで表され、化学ポテンシャルchemical potentialと言う呼び名がついている。
（25）
化学ポテンシャルは温度や圧力とは異なり、日常生活ではあまりなじみのない物理量であるが、（25）式を見ると、系にある粒子数の増減によるエネルギーの変化を表していることが示唆されている。これは平衡状態を表現するのにとても大事な量なのであとでまた議論しよう。
