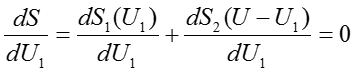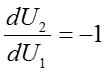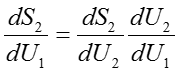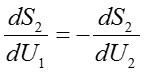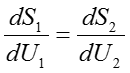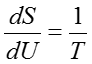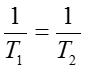いま、十分にマクロな量の気体分子を含む二つの部屋がある。ここで、熱のみを通す壁で仕切って二つの部屋を連結させることを想像してほしい。二つの部屋の外部から熱の流入、また外部への熱の流出はないものとする。すると、二つの部屋の間で熱の交換が起こり最終的に二つの部屋の温度は等しくなることは経験的にすぐ想像できる。ここでは、それを数学的に示そうと思う。
図4 二つの部分系からなる複合系
まず、それぞれの部屋に便宜的に部分系1、部分系2と名前を付ける。それぞれの部屋、つまり部分系が別々に平衡状態にあるとき、その系を特徴づける示量性変数が定義できる。そして、部分系1と部分系2からなる複合系を考えると、複合系の内部エネルギーUとエントロピーSについて、以下のような関係が成り立つことがすぐにわかる。
（42）
（43）
また、エントロピーは、エントロピーの自然な変数の関数として完全に記述できるので、以下のように書くことができる。
（44）
（45）
（46）
ただし、添え字は部分系の名前を示す。
ここで変数の動き方を少し整理すると、全体の内部エネルギーは外部と熱のやり取りがないので常に一定である。部分系の体積V1、V2と含まれる粒子数N1、N2もそれぞれ固定されていて動かないので、いま独立に動けるのはU1（もしくはU2）だけである。すなわち、（45）式と（46）式は以下のように表せる。
（47）
（48）
これらを踏まえると、複合系のエントロピーSは以下のようになる。
（49）
さて、それでは二つの部屋を連結してしばらく放置すると何が起こるであろうか。当然複合系としての平衡状態へと遷移するであろう。複合系が平衡状態にあるときSは最大値を取る。（49）式で定義されたSが最大値を取ることの必要十分条件はSのU1に関する微分係数が0になることである。つまり、
（50）
を満たすことが複合系の平衡状態の条件である。ここでちょっとした変数変換を行って式をすっきりさせることを試みると、まず（42）式より、
（51）
であり、両辺をU1で微分すると全体の内部エネルギーUは定数であるから
（52）
である。また、
（53）
なので、（52）式と組み合わせて次の式を得ることができる。
（54）
この式を（50）式に代入すると、複合系が平衡状態であることの必要十分条件は以下の式を満たすことに帰結する。
（55）
ここで、温度の定義式である（43）式に立ち返ると、体積Vと粒子数Nが固定された定数と見なせるときSはUの単変数関数とみることができ、次のような微分形式で書ける。
（56）
この関係を用いると、（55）式は部分系の温度についての条件を表す式となり、複合系が平衡状態にあれば次の式を必ず満たす必要がある。
（57）
つまり、熱のみを通すような壁で接した二つの系を放置しておくと平衡状態に達し、その時必ず温度が等しくなるのである。経験的には広く受け入れられる現象であるが、このように熱力学では数学的に厳密に示すことができる。
