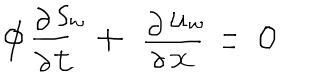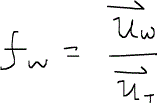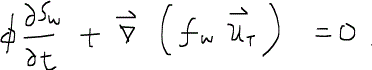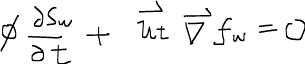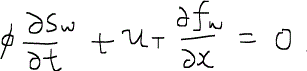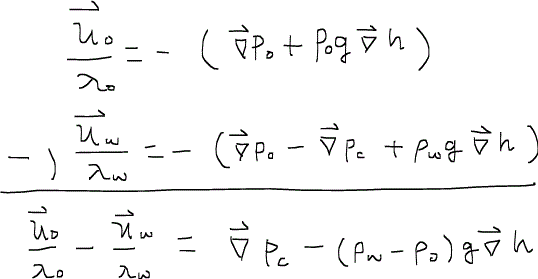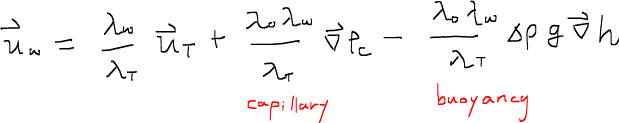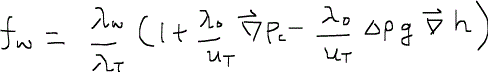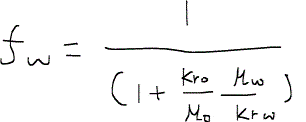ここまで二相流の流速について考えてきたが、求められた圧力方程式を解くだけでは、圧力の分布しか求められず、飽和率の分布は分からないままである。つまり、水の質量保存の式である、
（22）
を解く方法を考えることが次なる目標となる。そこでフラクショナルフローfractional flowという概念を導入する。
（23）
この式は水のフラクショナルフローを示しており、物理的な意味は全流速に対する水相の流速に他ならない。フラクショナルフローはスカラーである。このフラクショナルフローを用いると、水の質量保存の式は次のように書くことができる。
（24）
さらに左辺第二項は、積の微分法則を適用して次のようになる。
（25）
ただし、すでに求めたようにこの式の左辺第二項は常に0になるので結局、
（26）
となり、特に一次元においては、
（27）
なる式が導かれる。これはフラクショナルフロー表現の水に関する質量保存式mass conservation equation for water in fractional flow formと呼ばれている。
フラクショナルフローは流速の比であったが、限られた物性値で記述できるように中身を展開してみる。まず（14）式と（17）式を組み合わせて、圧力を消去する。
（28）
得られた式の形を整えると、水の流速について次の式が得られる。
（29）
もし、全流速uTが0でなければ、両辺をuTで除してフラクショナルフローの中身をついに明らかにできる。
（30）
なお、詳しくは重力数の記事で紹介するが、もしも重力と毛細管圧力の影響が無視できる場合（つまり、fw = λw/λTの場合）はフラクショナルフロー関数は、水と油の相対浸透率、粘性を用いて次のように書くことができる。ただしλは易動度であり、詳細については一つ前の易動度についての記事を参照のこと。
粘性が一定だと仮定すると、相対浸透率は飽和率のみの関数であるため、フラクショナルフロー関数も飽和率のみの関数になる。
