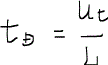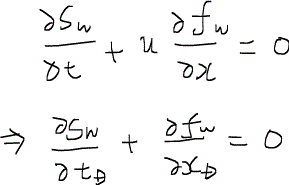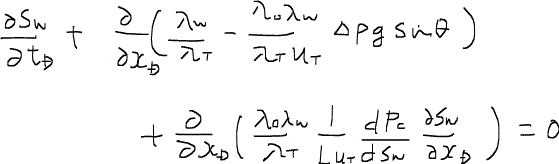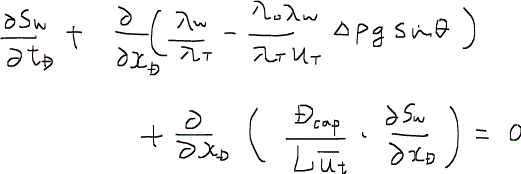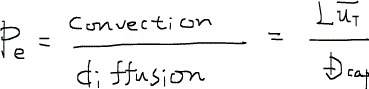まずは一次元問題を簡単にするために、時間と距離に関して次の無次元量を定義する。
xDは無次元距離dimensionless distance、tDは無次元時間dimensionless timeである。Lは一次元領域の長さ、下付き字のDは無次元量dimensionless numberであることを表している。つまり、一次元非圧縮非混和置換における水の質量保存式は
のようなシンプルな形に帰着する。この式にすでに求めたフラクショナルフロー関数を代入してみる。
ここで登場した係数の一部を纏めて、
と表し毛細管拡散係数capillary diffusion coefficientと呼ぶ。これを使って書き直すと、
また、さらに毛細管力項は以下のペクレ数Peclet number(Pe)なるものに依存していることが分かる。
すなわち、ペクレ数は移流項と拡散項の比を表しており、毛細管力項の相対的影響を決める重要な数字であることが分かる。例えば、Lが大きいと、毛細管力項の貢献度が下がる。すなわち、Lが数百メートルや数キロメートルオーダーになるフィールドスケールのシミュレーションでは、移流項のみを考慮し、毛細管圧力の影響は無視できる。シミュレータは毛細管圧力を考慮すると動作が非常に遅くなるため、無視できる場合に毛細管圧力を考慮してはいけない。
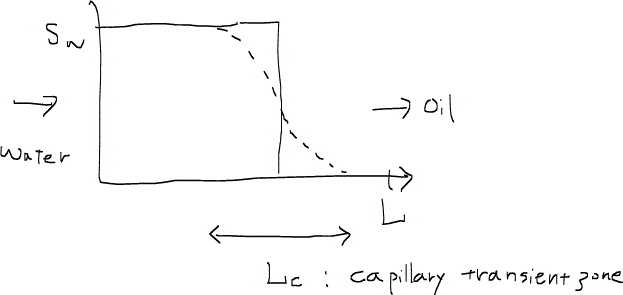
逆にコア実験などの比較的小さなスケールでは、毛細管圧力は無視できない。例えば実験室スケールでは毛細管遷移領域capillary transient zoneが無視できないスケールになり毛細管圧力を考慮して物理現象を考える必要がある。
なお、ここでのペクレ数は毛細管力についてのペクレ数であることを明示するために、時としてPe,cと表記される。