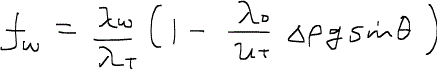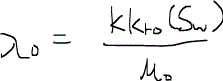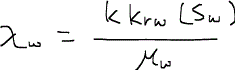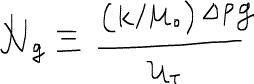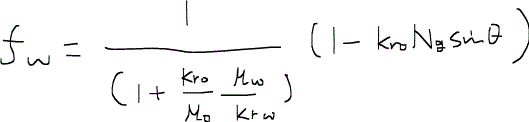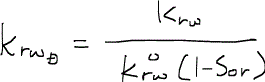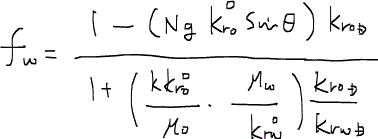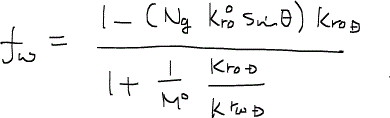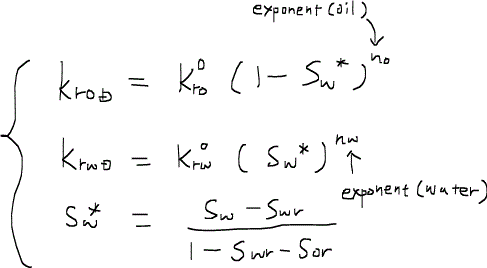さて、毛細管圧力が無視できる場合、フラクショナルフロー関数は次のように書くことができる。
（38）
ただし、
（39）
（40）
（41）
であり、θは貯留層の傾斜角dip angleである。また、重力数gravity number（Ng）を
（42）
のように定義すると、フラクショナルフロー関数は結局以下のようになる。
（43）
つまり、毛細管圧力の影響が無視できるときのフラクショナルフロー関数は、飽和率、重力数、傾斜角の関数であることが示されている。
（44）
なお、すでに与えられている定義を用いた簡単な演算より、
（45）
であることが分かるので、これを代入すると、フラクショナルフロー関数が実際に既知のデータから計算することが可能となる。
（46）
さらに、相対浸透率について、無次元相対浸透率dimensionless relative permeabilityなる概念を導入すると、次のように整理される。
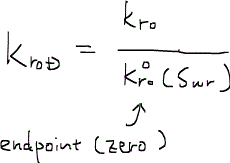（47）
（48）
無次元相対浸透率とは、相対浸透率をエンドポイントendpoint（相対浸透率の最大値）で除した値である。
（49）
次に、エンドポイントにおける易動度比mobility ratioをM0と表す。
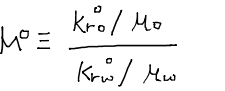（50）
この値を用いるとフラクショナルフロー関数は結局次の形となり、飽和率、重力数、傾斜角、易動度比の関数として与えられる。
（51）
相対浸透率を与える相関式はいくつも提唱されているが、例えばホナールプールHonarpourの式が有名である。
（52）
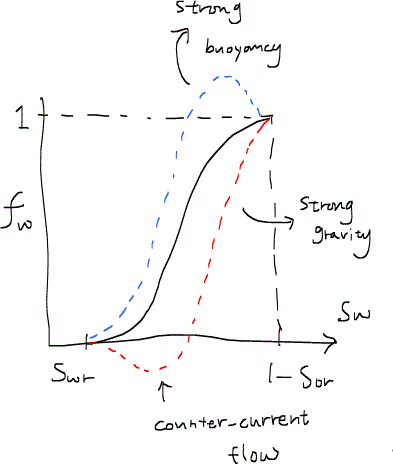
この式を使って、フラクショナルフロー関数をプロットすると、重力の影響が存在しない場合のS型の曲線形状になるが、重力数Ngやエンドポイントの易動度比M0の違いによって、その形状に異なった特徴が現れることが分かる。
重力数は粘性力と浮力の比（buoyancy/viscous force）である。もし重力数が大きければ、逆流現象counter-current flowが生じフラクショナルフロー曲線は負の領域に突入する。さらに浮力が極めて強いときはフラクショナルフロー曲線が1以上の領域に現れる。
また、エンドポイント易動度比が大きいときは掃攻効率が低くなる。この議論は重要なので別途展開する。
