少し前に、複数の相が共存している系が平衡状態であれば、示強性変数の![]() と
と![]() はどこでも同じになると述べた。これは経験的、実験的によく知られていることであり、ひとつの公理と言える。ところで、示強性変数には
はどこでも同じになると述べた。これは経験的、実験的によく知られていることであり、ひとつの公理と言える。ところで、示強性変数には![]() と
と![]() の他に化学ポテンシャル
の他に化学ポテンシャル![]() なる状態量があるのだった。相平衡において
なる状態量があるのだった。相平衡において![]() と
と![]() が与えられているときに(そしてその値が系のどこでも等しいとき)、
が与えられているときに(そしてその値が系のどこでも等しいとき)、![]() が満たすべき条件について突き詰めてゆく。つまり、相平衡状態における、
が満たすべき条件について突き詰めてゆく。つまり、相平衡状態における、![]() が満たすべき条件の導出をここではやってみようと思う。
が満たすべき条件の導出をここではやってみようと思う。
まず、![]() と
と![]() が与えられているとき、相
が与えられているとき、相![]() と相
と相![]() からなる閉じた系
からなる閉じた系![]() が二相共存の平衡状態にあるとする。
が二相共存の平衡状態にあるとする。
図5 二相共存の平衡状態
すると、それぞれの相についてギブズエネルギーの微分を計算すると、(100)式より次が得られる。
(107) ![]()
(108) ![]()
温度![]() と圧力
と圧力![]() が相
が相![]() と相
と相![]() で等しいのでその微分
で等しいのでその微分![]() と
と![]() はそれぞれの相で同じ値になる。それ以外の量にはそれぞれの相を示す下付き文字が入っている。一方、系
はそれぞれの相で同じ値になる。それ以外の量にはそれぞれの相を示す下付き文字が入っている。一方、系![]() についてギブズエネルギーの微分は同様に以下の式で得られる。
についてギブズエネルギーの微分は同様に以下の式で得られる。
(109) ![]()
ここで大切なのは、系![]() は閉じた系であり、含まれる粒子数は一定ということである。つまり、
は閉じた系であり、含まれる粒子数は一定ということである。つまり、
(110) ![]()
であるから、明らかにその微分は0になる。
(111) ![]()
したがって、(109)式は次の形になる。
(112) ![]()
次に、相![]() と相
と相![]() についてのギブズエネルギーの微分を表す(107)式と(108)式を足し合わせると、さしあたって次の式が得られる。
についてのギブズエネルギーの微分を表す(107)式と(108)式を足し合わせると、さしあたって次の式が得られる。
(113) ![]()
すでに議論してきたとおり、平衡状態において![]() 、
、![]() 、
、![]() は常に示量性変数なので、相
は常に示量性変数なので、相![]() と相
と相![]() からなる閉じた系
からなる閉じた系![]() の示量性変数の値はそれぞれの相における値の和で得られる。
の示量性変数の値はそれぞれの相における値の和で得られる。
(114) 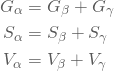
この関係を用いると、(113)式は系![]() についてのギブズエネルギーの微分の式として表すことができる。
についてのギブズエネルギーの微分の式として表すことができる。
(115) ![]()
系![]() についてのギブズエネルギーの微分の式はすでに(112)式があり、(115)式と常に同時に成り立つ必要がある。各項を見比べると、それぞれの式の左辺、右辺第一項、右辺第二項は同じ形をしており、(115)式から(112)式を引き算して得られる次の(116)式が恒等式になる必要がある。
についてのギブズエネルギーの微分の式はすでに(112)式があり、(115)式と常に同時に成り立つ必要がある。各項を見比べると、それぞれの式の左辺、右辺第一項、右辺第二項は同じ形をしており、(115)式から(112)式を引き算して得られる次の(116)式が恒等式になる必要がある。
(116) ![]()
このままだとここから先に進めないので、系![]() に関する情報を使えないかと考えてみる。
に関する情報を使えないかと考えてみる。![]() は相
は相![]() と相
と相![]() のみからなる閉じた系であり、系全体としての粒子は増えも減りもしない、という拘束条件が使える。
のみからなる閉じた系であり、系全体としての粒子は増えも減りもしない、という拘束条件が使える。
(117) ![]()
この式の微分をとると、![]() と
と![]() について次の式がとても簡単に得られる。
について次の式がとても簡単に得られる。
(118) ![]()
この関係を用いると、(116)式はさらに簡単になって、
(119) ![]()
となるので、結局相![]() と相
と相![]() が相平衡状態にあるときは、
が相平衡状態にあるときは、
(120) ![]()
が成り立つ必要があることが分かる。ここでは一成分二相の場合を考えたが、成分や相がいくつ増えても同じ関係が得られる。つまり、相平衡状態でならば、すべての相の化学ポテンシャルが成分ごとに等しくなる。
(121) ![]()
ただし、![]() は含まれる分子の種類数、
は含まれる分子の種類数、![]() は相の数を表している。
は相の数を表している。
また、詳しい説明は省くが、すべての相の化学ポテンシャルが等しい、ということは![]() と
と![]() が各相で等しい系における相平衡の必要十分条件である。すべての相の化学ポテンシャルが等しいと仮定すれば、ギブズエネルギーが相加的な示量性変数であることを示すことができるからだ。つまり、すべての相の化学ポテンシャルが互いに等しければその系は相平衡状態であり、その逆もまた然りである。ただし適用できる条件として、
が各相で等しい系における相平衡の必要十分条件である。すべての相の化学ポテンシャルが等しいと仮定すれば、ギブズエネルギーが相加的な示量性変数であることを示すことができるからだ。つまり、すべての相の化学ポテンシャルが互いに等しければその系は相平衡状態であり、その逆もまた然りである。ただし適用できる条件として、![]() と
と![]() が各相で等しいと仮定できる場合に限ることを忘れてはならない。
が各相で等しいと仮定できる場合に限ることを忘れてはならない。









